The Three-Stage Least Squares or 3SLS is applied to simultaneous equation models. It is different from single equation methods like Indirect Least Squares (ILS) and 2SLS because it is applied to all the equations of the model simultaneously. It estimates the parameters of all equations simultaneously, i.e. it is a systems method of estimation.
Related Posts
Logic behind 3SLS: 2SLS vs 3SLS
The 3SLS is more efficient as compared to the 2SLS method as it utilises more information. 2SLS is a single equation method and estimates coefficients using only the variables that appear in the model. On the other hand, 3SLS considers the entire structure of the model and the restrictions imposed by that structure on the parameters. 2SLS estimates one equation at a time, which means that it does not consider the correlations between error terms of different equations in the model.
Due to economic phenomenon and their interactions, it is common that the error terms of different equations in simultaneous equation models are correlated. This generally occurs because we include the most relevant variables in each equation. This implies leaving out the effects of other less relevant variables to be captured by the error terms. Since economic variables are interconnected in complex relationships, it is not surprising that the error terms of different equations end up being correlated.
Single equation methods cannot account for this information. Therefore, 3SLS is applied because it can be used to capture the relationships and correlations of error terms across different equations. 3SLS is an extension of the 2SLS technique and the first two stages of 3SLS are similar to that of 2SLS. If the error terms of different equations are not correlated, then, the 3SLS is reduced to the 2SLS.
Estimation of 3SLS
Before applying 3SLS, we must ensure that:
- The error terms of each equation must not be autocorrelated.
- The error terms of different equations are correlated, i.e. they are contemporaneously dependent.
- Lastly, the system of equations must be overidentified, which is usually the case in simultaneous equation models. We can ensure that with the help of Rank and Order Conditions of Identification.
Let us consider a simultaneous equation model with an “E” number of endogenous variables. The system will, therefore, have an “E” number of equations. We will denote the endogenous variables using “y” and the exogenous/predetermined variables by “x“. We further assume that we have a “k” number of exogenous variables in the model.
The 3SLS model is estimated in three stages as follows:
3SLS: Stage 1
We estimate the reduced form of all the equations in the model. We use all the endogenous variables as dependent variables and regress them on exogenous variables as independent variables.

Hence, the First Stage of 3SLS is similar to the First Stage of 2SLS. Similar to 2SLS, the estimated values of endogenous variables (from the First Stage) are used as instruments in the Second Stage.
3SLS: Stage 2
We use the estimated values of the endogenous variables as instruments in the Second Stage. That is, we substitute their values in place of endogenous variables that appear on the right side of the equations. For instance, we substitute y^1 in place of y1 wherever it appears on the right-hand side of the equations. In this way, we estimate every equation in the simultaneous equation model. This step is again similar to the estimation of 2SLS.
Thus, we have obtained the 2SLS estimates of all the coefficients. Using these estimates, we obtain the error terms or residuals of each equation in the model. Therefore, we obtain the estimates of the following:
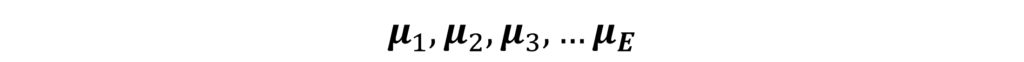
Each of these error terms contains “n” values because we have an “n” number of observations. For example, μ2 contains all the “n” errors corresponding to each observation in the 2nd equation. This is the point where the similarities between 2SLS and 3SLS end.
Using these estimates of residuals from Second Stage, we further compute the variances and covariances of all the error terms. The formula for computing covariance is as follows:

3SLS: Stage 3
Finally, we apply GLS or Generalised Least Squares to transform the original variables. Therefore, we use the variances and covariances of error terms to transform the variables in the original model to account for the correlations between the error terms of different equations.
Another common application of GLS is to eliminate the problem of heteroscedasticity and autocorrelation where we transform the original variables using the weights determined by the nature of heteroscedasticity or autocorrelation. We referred to that application as the Weighted Least Squares.
Here, we use the method of GLS to determine the nature of the relationship between error terms of different equations and transform the original variables. Additionally, the estimation of this 3SLS model can be carried out using statistical software packages that can easily deal with complex computations.
Econometrics Tutorials with Certificates
This website contains affiliate links. When you make a purchase through these links, we may earn a commission at no additional cost to you.



