The Dickey Fuller Test is a unit root based test of stationarity. The unit root based tests focus on the coefficient associated with the first lag of the time series variable. If the coefficient is one (has a unit root), then the time series behaves similarly to a Random Walk model which is non-stationary. Hence, we can statistically test whether that coefficient is equal to one. The Dickey Fuller Test, therefore, adopts this procedure by carefully manipulating equations to test for stationarity.
Econometrics Tutorials with Certificates
Deriving the Dickey Fuller test equation
Problem with a straightforward approach
First, let us consider the following model:
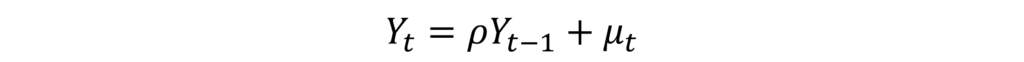
We know that the above model becomes a Random Walk Model without drift when ρ=1 and the time series will be non-stationary. In such a case, we say that the time series has a unit root.
For stationarity, therefore, we can test the coefficient value using the following hypothesis:

If we end up rejecting the null hypothesis after applying OLS, we will know that the time series is stationary. However, we face two major problems with this approach:
- Firstly, the usual t-test is not applicable to this model because it is autoregressive in nature and the results will not be accurate.
- Secondly, when testing the significance of coefficients after OLS, our null hypothesis is that ρ=0 and not ρ=1.
Solution: manipulating the equations
To overcome these problems, Dickey and Fuller further modified the equation as follows:

Now, we can apply OLS to this model and test the hypothesis of whether α=0.
Testing the hypothesis of stationarity
For stationarity, we can test the following hypothesis:
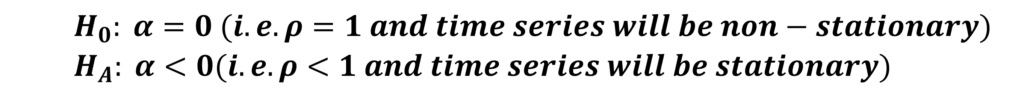
Therefore, the value of coefficient “α” should be negative and statistically significant if the time series is stationary.
To test its significance, we know that the t-test is not applicable because of the autoregressive nature of the model. A special statistic, known as the Tau statistic, is applicable and can be estimated as follows:

Furthermore, the critical/tabulated value of the Tau statistic can be obtained from the table developed by Dickey and Fuller. Later, the table was further extended by MacKinnon.
Including drift and trend in dickey fuller test
We also need to determine whether a time series has a deterministic trend and if it is trend stationary. Moreover, the time series may be stationary around a non-zero mean. As a result, we need to test stationarity using Dickey Fuller test on three different equations:
Dickey Fuller Test with drift and deterministic trend
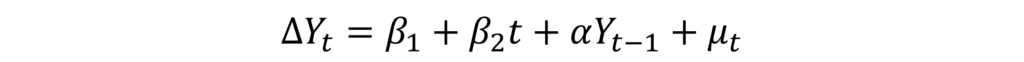
If the coefficient associated with the trend (t) is significant, then this equation should be used for hypothesis testing. Still, the interpretation of the test remains the same. That is, the coefficient “α” must be negative and significant for stationarity.
Dickey Fuller Test with only drift
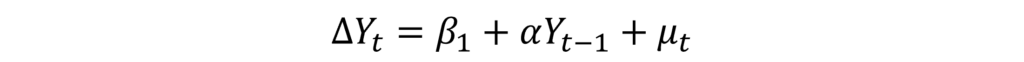
If the trend (t) coefficient is insignificant from the previous equation, we can remove it from the equation. Hence, the Dickey Fuller test will include only the drift component. Hence, if drift is significant, we can use the results of this equation for hypothesis testing. Similar to before, “α” must be significant and negative for the time series to be stationary.
Dickey Fuller Test without drift and deterministic trend
If both trend and drift are insignificant, we can move on to the original equation for hypothesis testing.
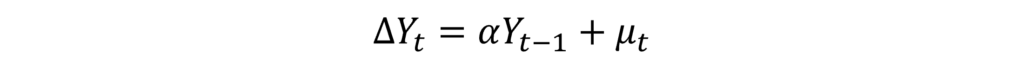
Again, the interpretation of the hypothesis testing and stationarity remains the same for the “α” coefficient.
drawback
Dickey and Fuller observed that their equations usually suffered from autocorrelated error terms. As a result, this undermined the results of the test because the models are unreliable under autocorrelation. To overcome this, they had to make changes to their equation by further including additional autoregressive terms. This changed test is known as the Augmented Dickey Fuller Test or ADF test.
Econometrics Tutorials with Certificates
This website contains affiliate links. When you make a purchase through these links, we may earn a commission at no additional cost to you.


