Breusch Pagan test for Heteroscedasticity

The Breusch Pagan test for heteroscedasticity is sometimes also referred to as the BPG or Breusch Pagan Godfrey test. It is one of the most widely known tests for detecting heteroscedasticity in a regression model. This test uses the squared residuals to run an auxiliary regression. The chi-square test is further applied after the auxiliary regression to check the presence of heteroscedasticity.

However, the Breusch Pagan test can be sensitive to the normality of error terms or residuals. Therefore, it is advisable to ensure that the residuals are normally distributed. The White test for heteroscedasticity can be considered an extension of the Breusch Pagan test because they share many similarities.

Econometrics Tutorials

application of the breusch pagan test

Step 1: Firstly, estimate the OLS model. Suppose, we have the following model with 3 independent variables:

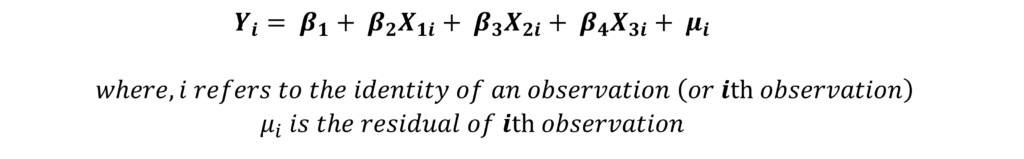
Step 2: Then, estimate the value of σ² with the help of residuals from the above model:

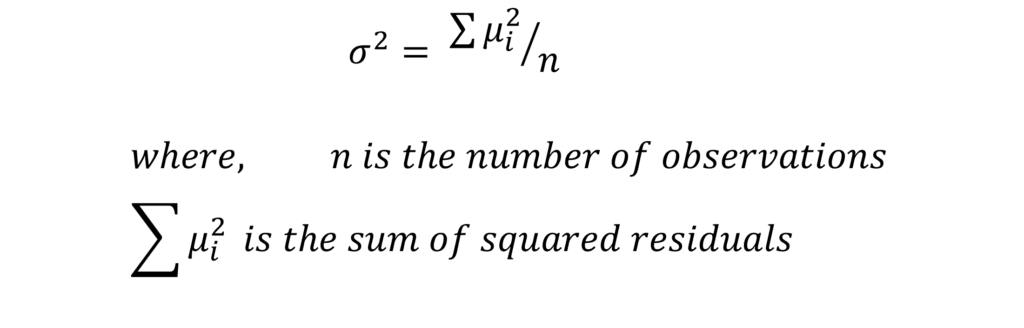
Step 3: Construct a new variable r_i. This variable will also be used to run the auxiliary regression later.

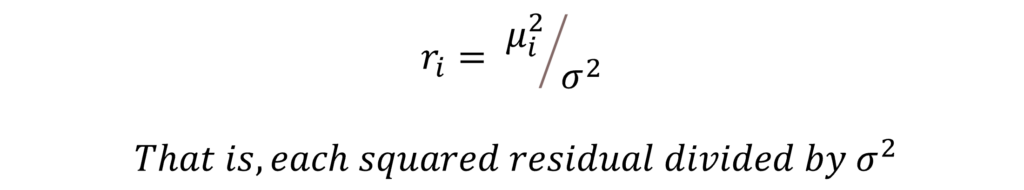
Step 4: run the auxiliary regression where we regress r_i on the independent variables:

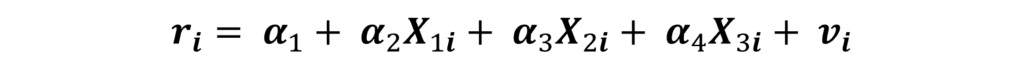
Step 5: Finally, calculate the explained sum of squares (ESS) and construct a new variable ω:

ω = 1/2(ESS)

The new variable ω follows a chi-square distribution. Furthermore, the degree of freedom is equal to the number of parameters used in the regression of r_i minus 1 (which is 4 – 1 = 3, in this example).

ω ~ 𝜒²_{d = k-1}

We reject the null hypothesis of homoscedasticity if the chi-square value of ω is greater than the critical chi-square value at the given level of significance.

Interpretation in practice

The Breusch Pagan test uses the following hypothesis:

H₀: Constant variance or homoscedasticity
H_A: heteroscedasticity

Breusch-Pagan Test
chi²	0.03
P-value	0.8618

Hence, we can reject the null hypothesis if the p-value is less than 0.05. However, if the P-value is greater than 0.05, we cannot reject the null hypothesis of homoscedasticity or constant variance. Here, the P-value is 0.8618 (that is, P-value > 0.05) in the above example. This further means we cannot reject the null hypothesis of constant variance. Hence, there is no evidence of heteroscedasticity.

Disadvantage: finally, the Breusch Pagan test results can be unreliable if the residuals are not normally distributed. Therefore, this test should not be applied in such a case and we have to rely on other tests of heteroscedasticity.

Econometrics Tutorials