The production of all goods and services is carried out using certain inputs. These inputs include the labour, capital and raw materials used in producing the given good or service. The production function expresses the use of these inputs to produce the output in a mathematical and graphical form. It is a key concept in Economics which is used to study the behaviour of firms and industries. Moreover, production functions are also employed in the study of growth and development.
Econometrics Tutorials with Certificates
Definition of Production Function
The production function is the mathematical representation of the relationship between inputs and outputs involved in the production process. It is used to describe the amount of output that can be produced using different combinations of the given inputs. In other words, we can say that it shows the maximum output that can be produced with the available inputs.
Famous Economist Paul Samuelson defined production function as follows:
The production function is the technical relationship between physical inputs and physical outputs, ceteris paribus. It describes the maximum feasible output of a firm or an economy, for every possible combination of inputs, given existing knowledge and technology.”
Paul Samuelson in “Economics: An Introductory Analysis,” 13th Edition, published in 1989, Page 372, Chapter 9
This definition emphasizes certain assumptions and conditions that are necessary for defining the production function. “Ceterus Paribus” shows the importance of considering all other factors as constant. When we study the relationship between inputs and output, we must take other factors to be given. This also includes the level of technology and knowledge. This is because a change in technology can alter the relationship between inputs and output.
Economists use several production functions to study the production process. Some of the most commonly used production functions include the Cobb-Douglas Production Function, the CES production function, the Leontief production function and the VES and translog production function. Each of these functions has its own set of assumptions and restrictions which we will discuss later.
Short-run and long-run production functions
Short-run
In the short run, it is not possible to change or adjust all the inputs. Some of the inputs remain constant in the short run. For example, a firm cannot expand its factory in the short run. However, it can still increase or decrease the amount of labour employed. As a result, some inputs are variable whereas others are fixed in the short run. Generally, labour is considered a variable factor and capital is considered a fixed factor in the short run.
The short-run production function, therefore, describes the relationship between the number of inputs and the quantity of output produced when at least one input is fixed.
In other words, it is a mathematical equation that shows the maximum amount of output that can be produced from a given amount of variable input (such as labour), given the fixed input (such as capital). This function typically exhibits diminishing marginal returns which means that as the variable input increases while the fixed input remains constant, the marginal product of the variable input eventually decreases. That is, the additional output produced from each additional unit of the variable input starts falling after a certain point and even becomes negative in the end. This is also discussed in detail in the Law of Variable Proportions.
Long-run
In the long run, all the factors of production or inputs are variable. The producers are free to expand their scale of production by increasing the capital in the long run. It represents the maximum output that can be produced using any combination of inputs, given the state of technology and the prices of inputs.
Long-run production function typically exhibits decreasing, constant or increasing returns to scale. This means that as all inputs are increased in proportion, the output increases by less proportion, the same proportion or more. Hence, this reflects the fact that as a firm grows and expands its operations, it can take advantage of economies of scale. Economies of scale can be realised through lower costs of production and higher efficiency, which further enable the producers to make more output at a lower cost per unit.
Difference between short-run and long-run production functions
- Time horizon: The short-run production function considers a period where at least one input is fixed and cannot be changed. Meanwhile, the long-run production function considers a period where all inputs are variable and can be adjusted freely.
- Adjustment of inputs: In the short run, a firm can only adjust its variable input such as labour. The fixed input such as capital equipment remains constant. In the long run, all inputs can be adjusted or varied freely to maximize output.
- Marginal returns: The short-run production function operates on diminishing marginal returns, where the additional output produced by each additional unit of the variable input eventually decreases. In contrast, the long-run production function shows decreasing, constant or increasing returns to scale. With changes in inputs, the output can increase by the same proportion as the change in inputs, less than that proportion or even more.
- Flexibility: The long-run production function provides a more flexible framework for firms to optimize their production processes and adapt to changing market conditions and technology. The short-run production function provides a more rigid framework due to the presence of fixed inputs.
- Planning horizon: The long-run production function enables firms to plan for the future and make long-term investments in new technologies, equipment, and facilities. The short-run production function, however, focuses on maximizing output in the current period with the current level of technology, equipment and facilities.
Types of production functions
Some of the most commonly used production functions in economic analysis are as follows:
Cobb-Douglas Production Function
The Cobb-Douglas production function is the most widely known production function in Economics. It is often used in studying production behaviour and can be expressed as:

This function was introduced by Charles Cobb and Paul Douglas in the 1920s. Some of the important properties of the Cobb-Douglas production function can be briefly stated:
- It is a linear and homogenous function.
- It can be used to model constant, increasing and decreasing returns to scale.
- The Elasticity of substitution of this function is 1.
- It exhibits diminishing marginal returns to a factor if the other factor of production is held constant.
- This function can be extended to include other inputs or factors of production.
Finally, the major drawback of the Cobb-Douglas production function is that its elasticity of substitution is 1. This is unrealistic because we practically never observe this in reality. Therefore, the CES production function tries to overcome this shortcoming. The Elasticity of substitution in the CES function is not unity, however, it is still constant.
CES Production Function
The CES production function is another widely used function in Economics. The CES in its name stands for Constant Elasticity of Substitution. As the name suggests, the elasticity of substitution in this function is constant. Hence, It provides more flexibility as compared to the Cobb-Douglas production function and can be expressed as:

The important properties of the CES function are:
- It is a homogenous function of degree 𝜃.
- The elasticity of substitution is constant and does not have to be 1. This is different from the Cobb-Douglas production function which has the elasticity of substitution equal to one.
- The Cobb-Douglas production function is a special case of the CES production function. That is, CES reduces to the Cobb-Douglas function when the substitution parameter (𝛿) approaches 0 in the limit.
- It can also be used to model constant, increasing or decreasing returns to scale. The returns to scale depend on the degree of homogeneity of the function. CES shows constant returns to scale if θ = 1. We can observe increasing returns when θ > 1 and decreasing returns to scale when θ < 1.
Leontief Production Function
The Leontief production function assumes that the output can only be produced using fixed proportions of inputs. It was developed by Wassily Leontief in the 1930s. The Leontief production function can be expressed as:
Q = min(𝛼L, 𝛽K)
where Q is output, L is labour, K is capital,
𝛼 and 𝛽 represent the fixed proportions of labour and capital needed to produce a unit of output
The Leontief production function assumes that one unit of output can only be produced by using a certain quantity of labour and capital. There is no flexibility to vary the relative amounts of the inputs. For example, this function can apply to baked goods like a muffin. One unit of muffin will need an exact amount of ingredients which cannot be varied. Suppose, the muffin recipe needs 250 grams of flour and 1 egg to produce 1 unit. As a result, tt does not matter if the chef has 5 Kg of flour. If the chef has only 3 eggs, he/she will be able to produce only 3 muffins because these ingredients can only be used in fixed proportions.
This production function is applicable to specific situations and has the following important properties:
- The input proportions are fixed and cannot be varied.
- The function exhibits constant returns to scale. The output will increase by the same proportion as the increase in inputs.
- The marginal productivity of inputs is zero. Since the input proportions are fixed, increasing only one input will not increase the output.
VES Production Function
The VES production function stands for variable elasticity of substitution. In the earlier production functions, we observed that the elasticity of substitution was one or constant. However, the VES function attempts to remedy this shortcoming by allowing the elasticity of substitution to change with a change in inputs. In this function, the elasticity of substitution also depends on the level of inputs being employed. The VES production function can be expressed as follows:
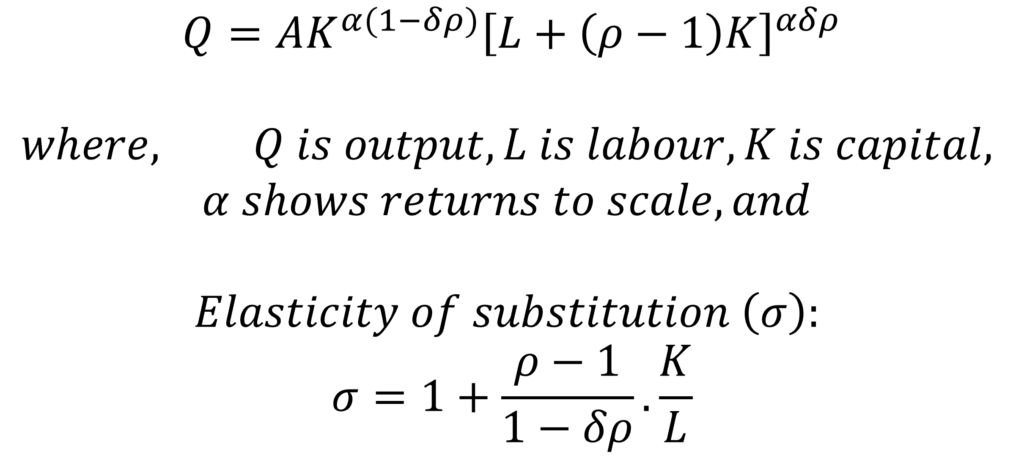
Moreover, it is important to note here that the VES production function has other forms as well. Another commonly used form of the VES function is:
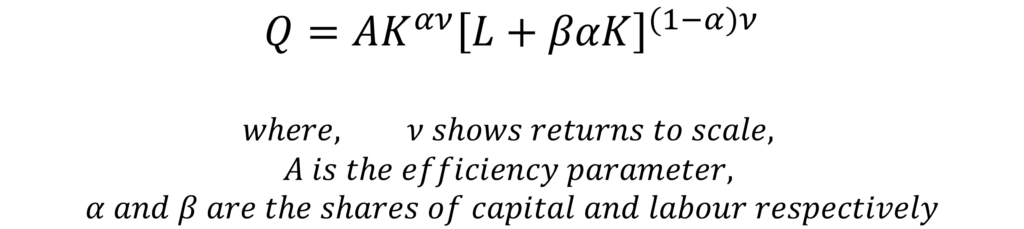
The VES production function has the following properties:
- VES is a homogenous function.
- It can be used to model constant, increasing or decreasing returns to scale depending on the value of the returns to scale parameter.
- The VES production function reduces to the Cobb-Douglas production function when 𝜌 = 1.
- It has a variable of elasticity of substitution which gives more flexibility in understanding the production behaviour.
Translog Production Function
The Translog Production function is a very flexible form of the production function and can be used to model variable elasticity of substitution. In its general form, the translog production function can be expressed as:

Suppose, we have two inputs – labour and capital, then we can write the translog production function as follows:
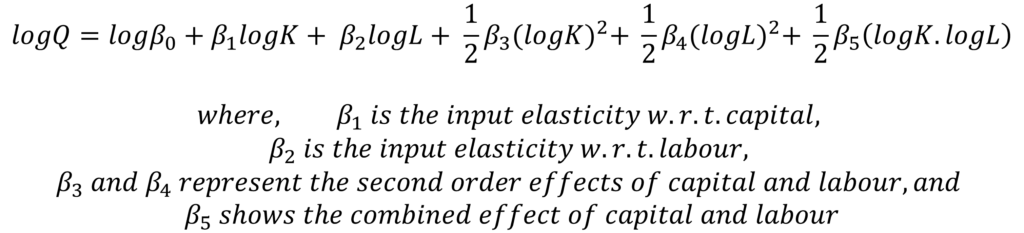
This function will reduce to a Cobb-Douglas production function if the second-order effects and the combined effects are zero. Therefore, it becomes a Cobb-Douglas function when 𝛽3 = 𝛽4 = 𝛽5 = 0.
As evident from its general form, the translog production function can be easily extended to include any number of inputs. Moreover, it can model variable elasticity of substitution as well as all types of returns to scale. The translog production function is only homogenous under certain restrictions and you can learn more about it here.
Econometrics Tutorials with Certificates
This website contains affiliate links. When you make a purchase through these links, we may earn a commission at no additional cost to you.


