The Probit Model is used when we have a binary or qualitative dependent variable in the model. Similar to the Logit Model, the Probit Model overcomes the difficulties or problems of the Linear Probability Model. It is not advisable to apply OLS or LPM when we have a dependent variable that is binary or qualitative. This is because the results of LPM suffer from serious problems that can be solved by applying the Logit and Probit Models.
The Linear Probability Model or LPM produces heteroscedastic residuals with non-constant variance. This undermines the tests of significance and makes them unreliable. Further, the probabilities obtained from the LPM can exceed the limits of 0 and 1. A probability greater than 1 or a negative probability does not make sense. Finally, OLS or LPM assume a linear relationship between the dependent and independent variables.
This linearity assumption is not realistic as discussed in the Logit Model and the Logit and Probit Models. In reality, the change in probability with a change in the independent variable will not be constant. Instead, this change in probability should be different at different levels of independent variables. At extreme values of independent variables, the change in probability should be smaller or slower. This implies a non-linear relationship between dependent and independent variables.
Probit Model and Normal CDF
We apply the Probit Model using the Normal CDF. The logic behind the Logit and Probit models is the same, the only difference lies in the functional forms. The logit model uses the Sigmoid function, whereas, the Probit Model uses the Normal CDF. The Normal CDF or Normal Cumulative Distribution Function is derived from the normal distribution. It is useful when we have binary or qualitative dependent variables because it helps solve the problems of LPM.

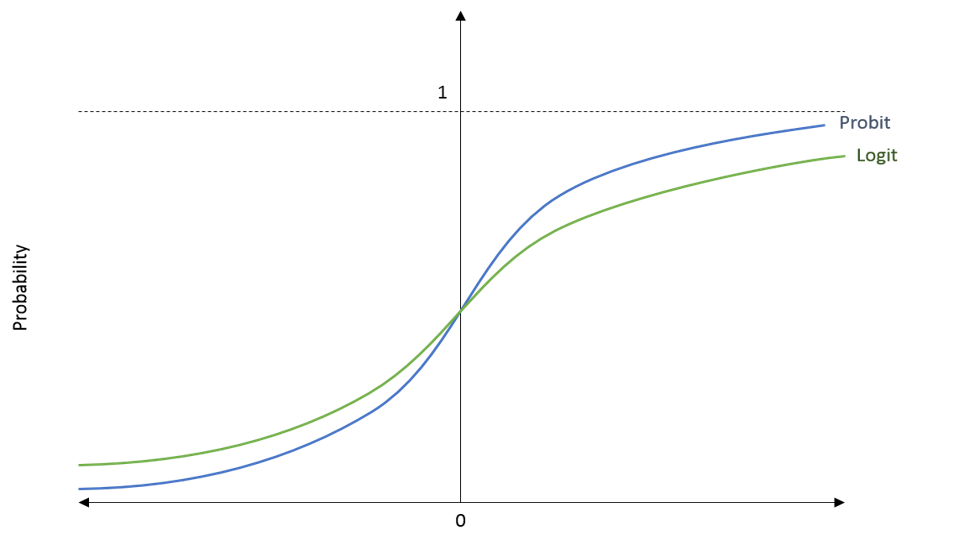
The general shape of the Sigmoid (logit) and Normal CDF (Probit) is shown in the diagram. The probability (Pi) is shown on the y-axis and the value of Zi is shown on the x-axis. The Zi is defined in the Sigmoid and Normal CDF formulas above. When we estimate the Logit or Probit model, we obtain this Zi value from the independent variables and the model equation.
As we can see, the functions never exceed the limits of 0 and 1. They keep getting closer but never cross these limits of probability. Moreover, they help incorporate non-linear behaviour in the model. The probability changes faster in the middle part of the diagram. On the other hand, the change in probability is slower or smaller as we approach extreme values on the right or left tail. Therefore, these functions overcome the critical problems discussed in the Linear Probability Model.
Probit Model Estimation
Let us consider the same model we used to illustrate the Logit Model:
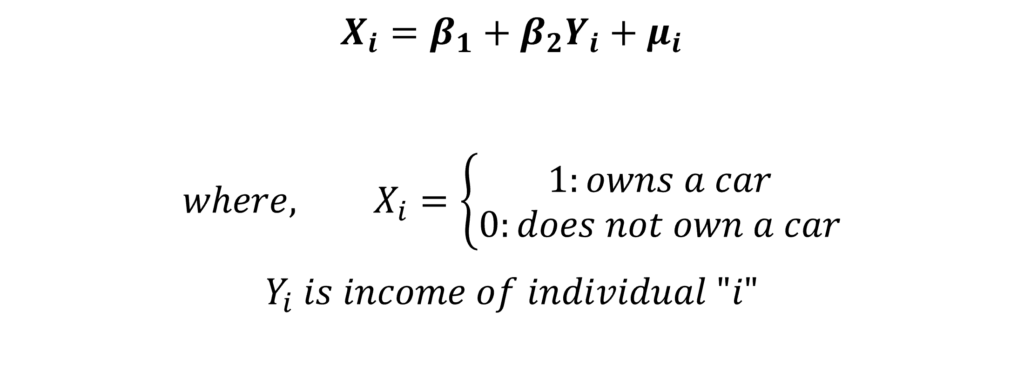
The dependent variable is binary or qualitative in nature. That is, X is equal to 1 if the individual owns a car and 0 if the individual does not own a car. Further, we can see that X is a function of the independent variable income (Yi). We can include other independent variables in the model such as marital status, daily distance travelled etc. However, we have included only 1 independent variable income for simplicity.
We know that OLS or LPM are not appropriate for such a model with a binary dependent variable. Therefore, we have to estimate it with the Logit or Probit Model. In the case of the Probit model, we use the Normal CDF to project the model equation as:

The model equation with the coefficients and the independent variables gives us Zi. That is, Zi is a function of the independent variables (income Yi in this example). Further, Pi or the probability of owning a car is a function of Zi. Moreover, it is important to note here that Zi is a linear function of Yi or the independent variables. Whereas, Pi is a non-linear function of Zi.
Maximum Likelihood Estimation
Similar to the Logit model, we estimate the Probit model using the Maximum Likelihood approach. The likelihood and log-likelihood functions for Probit are derived under the same assumption i.i.d. That is, the observations must be identically and independently distributed. A complete derivation of the likelihood function and the details about the assumptions are available in the Video Tutorial Series on the Logit and Probit Models.
The log-likelihood function for the Probit Model can be expressed as:
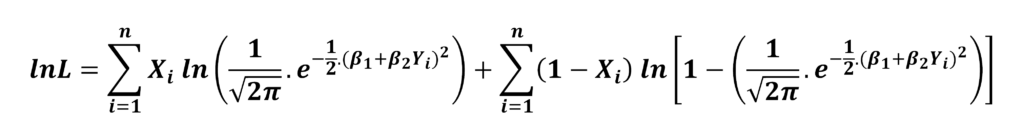
The logic behind the Maximum Likelihood approach is that we have to obtain the values of parameters in such a way that the probability of observing the sample values of X is at the maximum. To accomplish this, we estimate the coefficients by maximizing the log-likelihood with respect to the parameters of the model (β1 and β2 in this example).
Probit Model Interpretation and Marginal Effects
The coefficients and their direct interpretation do not make much economic sense in the Probit Model. The estimated coefficients show the change in the Z score with a 1 unit change in independent variables. This is different from the Logit model where the coefficients show the change in log odds. However, they are similar in the sense that direct interpretation is not very useful in both models.
As a result, we often calculate the marginal effects after the logit and probit models. The marginal effects show the change in probability due to a small change in the independent variable. In our example, the marginal effect will be a change in the probability of owning a car due to a small change in income. The marginal effects are calculated as the partial derivative of the probability with respect to the independent variable.
In OLS, the coefficients themselves are the marginal effects of the given independent variable on the dependent variable. This is because the partial derivative in the case of OLS is simply the coefficient of the independent variable. But, this is not true for logit and probit models and we have to estimate the marginal effects separately.

As we can see, the marginal effect in our example will be the partial derivative of probability Pi with respect to the independent variable Yi. This can be calculated easily using statistical software programs.
Types of Marginal Effects (MEMs, AMEs, MERs): Importance of the level of independent variables
We know that the relationship between the probability and the independent variables in non-linear. This means that the change in probability (or marginal effects) will be different at different levels of the independent variables. In our example, this would mean that the change in the probability of owning a car due to a change in income will be different depending on the level of income.
Therefore, the marginal effects are different at different levels of independent variables. At extreme levels, the probability changes slowly. For instance, at a very high or very low income, the change in probability due to a change in income will keep getting smaller as we approach further extreme values of income. This brings us to an important choice that we must make while estimating the marginal effects.
We must choose the levels of independent variables at which we want to estimate the marginal effects. This choice usually depends on the objectives of our research and we can choose some values that make sense based on our aims. In general, we have the option to estimate the Marginal Effects at Mean (MEMs), Average Marginal Effects (AMEs) and Marginal Effects at Representative Values (MERs). Each of these has its advantages and disadvantages. A complete derivation, choosing which marginal effects to estimate, their application and interpretation are available in the Video Tutorial Series on the Logit and Probit Models.
Econometrics Tutorials with Certificates
This website contains affiliate links. When you make a purchase through these links, we may earn a commission at no additional cost to you.



