Economists James Durbin and Geoffrey Watson developed the Durbin Watson test in the early 1950s. They introduced the test in their paper “Testing for Serial Correlation in Least Squares Regression: I,” published in 1950 in the Biometrika journal.
The Durbin Watson test detects autocorrelation in the residuals of a regression analysis. Autocorrelation occurs when the residuals (errors) from a regression analysis are correlated with each other. In other words, it indicates whether there is a pattern in the residuals that suggests that the assumption of independent errors has been violated.
Econometrics Tutorials with Certificates
Estimating The Durbin Watson Test Statistic (d)
Firstly, the Durbin Watson test is applied to the First-order Autoregressive scheme where the errors are related to the previous period error. Furthermore, this test does not work well with higher-order autoregressive schemes. To illustrate the test in detail, let us continue with the model we considered in the post about Autocorrelation. Suppose, we have the following model:
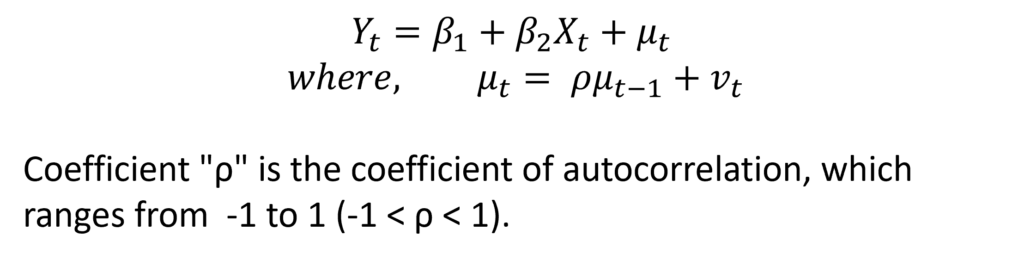
Hence, the error term (μt) is correlated with its lagged value. Also, the first-order autoregressive scheme means that it is dependent on the previous one-period error (μt-1). The coefficient “ρ” is the coefficient of autocorrelation, which further ranges from -1 to 1 (-1 < ρ < 1).
Calculation of the d statistic
The Durbin Watson d for the model shown above:
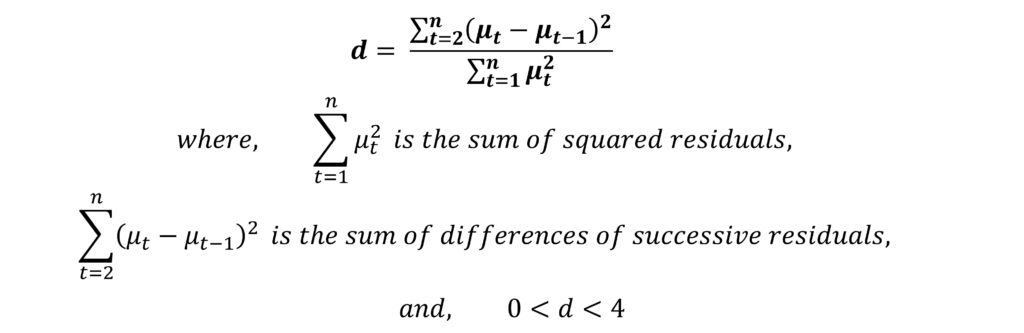
Firstly, this “d” statistic lies between 0 and 4 and a value of 2 indicates no autocorrelation in the residuals. At d = 2, the autocorrelation coefficient ρ = 0. When this autocorrelation coefficient ρ = 1, then the “d” statistic is 0. On the other hand, d = 4 when ρ = -1.
| Autocorrelation Coefficient (ρ) | Durbin Watson d statistic | Autocorrelation |
| 0 | 2 | No autocorrelation |
| +1 | 0 | Perfect positive autocorrelation |
| -1 | 4 | Perfect negative autocorrelation |
Therefore, a value of 2 for the Durbin-Watson d statistic is desirable because it indicates the absence of autocorrelation in the model. Moreover, we know from the above table that the values of “d” and “ρ” are related. We can define this relationship as:
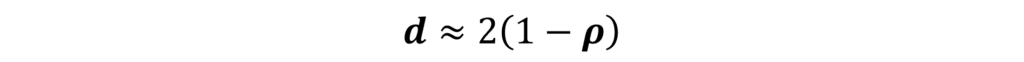
Critical Values of d
The “d” statistic does not follow any particular distribution. However, Durbin and Watson gave upper and lower limits of “d” for a different number of observations and explanatory variables. Durbin-Watson table shows these critical values of “d”. Moreover, the estimated statistic must lie between these critical limits.
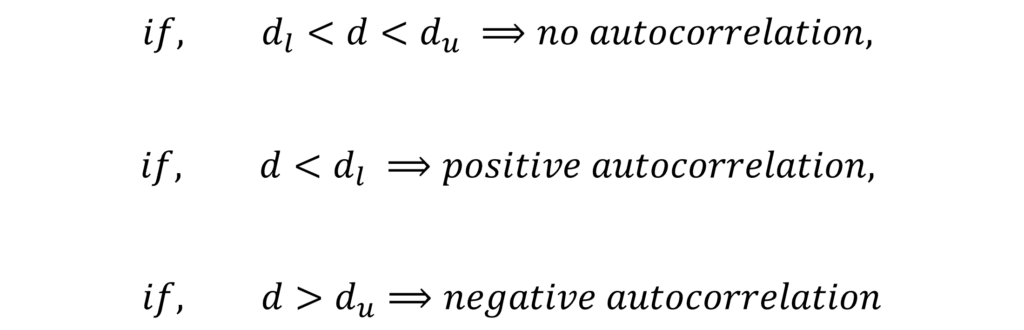
Limitations of the Durbin Watson test
- Firstly, the Durbin Watson test can be used to detect autocorrelation in the first-order autoregressive scheme only. Hence, it cannot be used in the case of higher-order autoregressive schemes.
- Secondly, the errors or residuals must be normally distributed for the application of this test. If the errors are not normal, then the results of the test may be biased.
- Finally, to apply the Durbin Watson test, the model should not include the lagged dependent variable as one of the independent variables.
Despite these limitations, the Durbin-Watson test remains a widely used and valuable tool for detecting autocorrelation. This is particularly true in cases where the assumptions of the test are met and interpreted cautiously in conjunction with other diagnostic tests.
Econometrics Tutorials with Certificates
This website contains affiliate links. When you make a purchase through these links, we may earn a commission at no additional cost to you.


