The White test is one of the most commonly used statistical methods of detecting heteroscedasticity. It focuses on analysing the residuals from regression models to check for heteroscedasticity. Furthermore, the test is based on the Chi-square distribution to test its hypothesis. Generally, it is used in conjunction with other methods such as graphical analysis to detect heteroscedasticity.
Econometrics Tutorials with Certificates
application of the white test
Step 1: estimate the OLS model. Let us consider the following model:
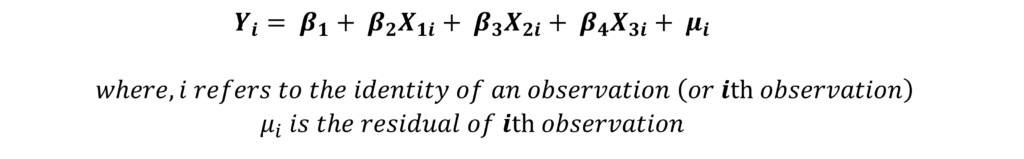
Step 2: estimate the squared residuals μi2. After estimating the model and obtaining the residuals, you must square the values of all the residuals. These squared residuals are used to run another regression.
Step 3: run the following regression:
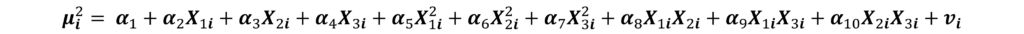
This regression includes the independent variables from the original models, squares of all those variables and their cross-products.
Step 4: obtain the R2 for this regression. The R2 value from this second regression is used to calculate the chi-square value later.
Step 5: Calculate the chi-square value of “n.R2 “, where ‘n’ is the number of observations. The degree of freedom for chi-square equals the number of independent variables in the regression of μi2 (in this example, degree of freedom = 9).
n.R2 ~ 𝜒2d=9
If the chi-square value obtained in this way is greater than the critical chi-square value, we reject the null hypothesis of homoscedasticity, i.e. heteroscedasticity exists. On the other hand, if it is less than the critical chi-square value, we conclude that there is no heteroscedasticity. In this example, it will also mean that α2 = α3 = α4 = …………= α10 = 0.
Implementation in practice
The White Test can be easily carried out using statistical software packages. The output of the test looks similar to the following:
| White Heteroscedasticity Test | |
| chi2 | 10.00 |
| P-value | 0.3505 |
H0: homoscedasticity or constant variance
HA: heteroscedasticity exists
If the p-value is less than 0.05, we can conclude that heteroscedasticity exists. In this example, however, the p-value is greater than 0.05. Therefore, heteroscedasticity is not a problem here.
Limitations and advantages of the White Test
Limitations
- The test usually requires a large sample, especially if there are a lot of independent variables in the model. This is because the test estimates the squares as well as cross-products of all the independent variables. This can restrict the degrees of freedom.
- The White test can also act as a test of specification error. As a result, the significant test statistic might be due to specification errors rather than heteroscedasticity. You must drop the cross-products from the test equation to test purely for heteroscedasticity.
Advantages
This test does not depend on the normality of error terms and it does not require choosing ‘c’ or ordering observations (Goldfeld-Quandt test). Hence, it is easy to implement in most cases.
Related Posts
- Heteroscedasticity: Causes and Consequences
- Breusch-Pagan Test for Heteroscedasticity
- Goldfeld-Quandt Test for Heteroscedasticity
- Weighted Least Squares Estimation
Econometrics Tutorials with Certificates
This website contains affiliate links. When you make a purchase through these links, we may earn a commission at no additional cost to you.



Hello, I’m Sari! I want to know about previous studies such as books or journals state that “The degree of freedom for chi-square equals the numbers of the independents-variable in the regression of U2T”. However, in other sources it is stated that degree of freedom or df=k-1 (k= the original number of independent variables).
Thank you very much and this will greatly assist me in completing my thesis 🙂
Hello, Sari. Generally, we include original independent variables, squares of those independent variables and their cross-products in the regression of u2t. But in some cases, we can apply the White test without the cross-products to test purely for heteroscedasticity. This variation will only include the original independent variables and their squares in the regression of u2t (because cross-products are not included). The degree of freedom then, would be equal to the original independent variables and their squares.
Sometimes, this is also written as “df = k – 1”, where k = number of parameters which also includes the constant. Please check if this is the case in the sources you mentioned. Alternatively, it would be great if you can share those sources so I can take a look.