Identification: Rank and Order Conditions

A simultaneous equation model is said to be identified if we can obtain unique estimates of the coefficients in the model. The equations in identified models have a unique structure or statistical form. It is essential to determine the identification of simultaneous equations models before estimation. For this purpose, the Rank and Order Conditions are used.

2SLS Video Tutorial Series

3SLS Video Tutorial Series

meaning of identification

Problem of Identification

Let us take the example of demand and supply theory to illustrate the problem of identification:

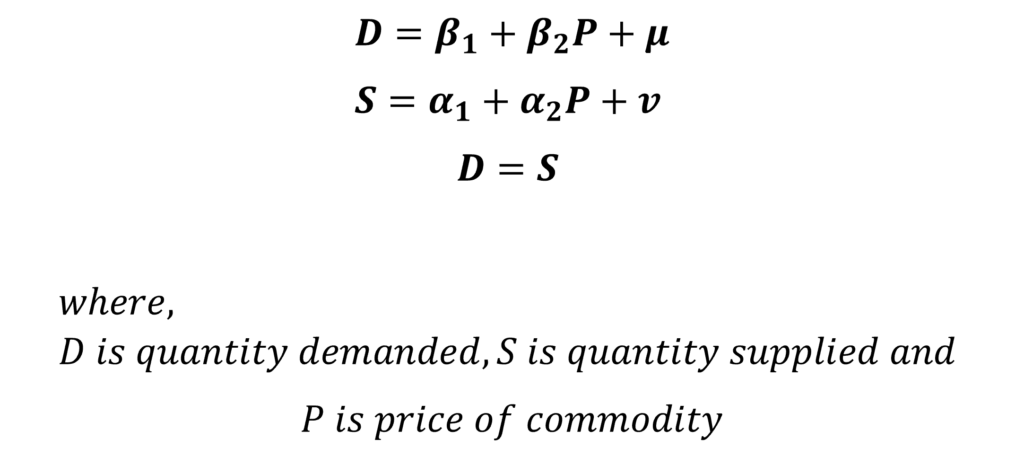
In this model, the first equation is the demand function, the second is the supply function and the third equation represents the equilibrium. Hence, we have 3 equations and 3 endogenous variables in the model.

However, both the equations of demand and supply function are identical. In practice, the quantity supplied at any time is the same as the quantity demanded. This is because we always have the data on the quantity bought of a commodity at a given price, which shows the equilibrium of demand and supply. In other words, our sample observations show the quantity demanded and quantity supplied simultaneously, at a given price.

If we estimate the equations, we cannot differentiate between the coefficients of the demand function (B₁ and B₂) and the coefficients of the supply function (a₁ and a₂). Then, how do we identify the demand function or the supply function? This is the problem of identification in simultaneous equation models. Our equation may be the demand function or the supply function and we cannot distinguish between the two.

Making the Equations Identified

To estimate such a model, we need to make all the equations in the model identified. This means that we need to make them unique or give them a unique statistical form. To do this, we need to include other variables in the model that are specific to each equation. For instance, we can include the income or assets in the demand function. In the supply function, we can include variables like the price of factor inputs (such as wages) or weather conditions in the case of agricultural products. Therefore, these variables will make the equations unique and enable us to identify the functions.

For example, changes in income will shift the demand function, while the supply function will remain fairly stable. Therefore, we can identify the supply function with the help of the variable excluded from its equation (income variable in this case). Similarly, we can identify the demand function using the variables excluded from it, such as the weather conditions and factor prices which will shift the supply function and the demand function will remain stable.

This is known as the paradox of identification because we identify a function with the help of variables that are excluded from it, but, included in other equations of the simultaneous equation model. Hence, we need to ensure that our model is identified before estimating it with any simultaneous equation techniques.

Rank and order conditions to determine identification

We use the Rank and Order Conditions to identify whether a simultaneous equation model is underidentified, exactly identified or overidentified.

If an equation in the model does not have a unique statistical form, it means that the equation is underidentified. On the other hand, an identified equation has a unique statistical form and can either be exactly identified or overidentified. Moreover, we may need to employ different estimation techniques for exactly identified and overidentified models. The method of Indirect Least Squares (ILS) can be used to estimate coefficients of exactly identified models. However, ILS cannot be applied to overidentified models, which need to be estimated using other methods like 2SLS, 3SLS or Maximum Likelihood techniques.

Order Condition

The Order Condition is necessary but not a sufficient condition for the identification of the chosen equation. The formula for Order Condition is as follows:

If this condition is not satisfied, we conclude that the equation is underidentified. If this condition is fulfilled, we move on to test the Rank Condition. Hence, the Order condition alone is not sufficient for identification.

Rank Condition

The Rank Condition states that an equation is identified if it has at least one determinant that is non-zero, from the matrix constructed by excluding coefficients from the given equation, but including coefficients in other equations of the model.

Hence, we need to construct a matrix of coefficients that contains only the coefficients of variables that are not present in the equation under consideration. Then, we calculate the determinant of that matrix which will be of the order (E-1). If any of the determinants is non-zero, we conclude that the equation is identified. Conversely, if every possible determinant is zero, then the equation is underidentified.

Implementation of rank and order conditions of identification

To illustrate the implementation of these conditions, let us take the example of the following model:

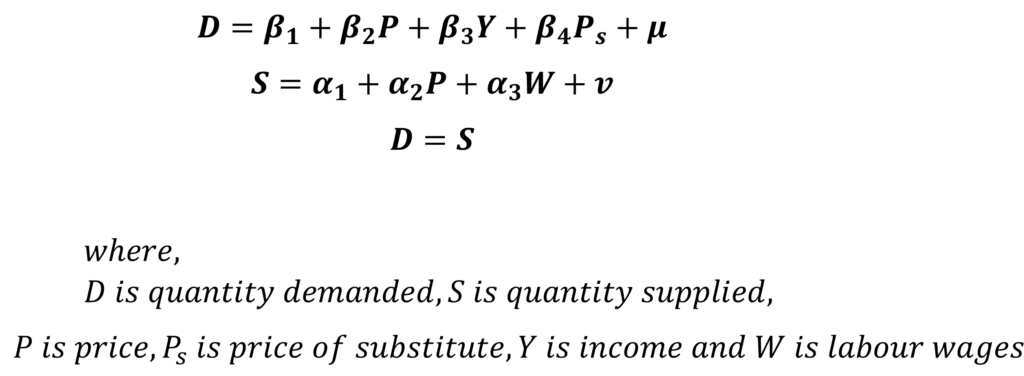
This model is complete because it contains 3 equations and 3 endogenous variables (D, S and P). Furthermore, the variables P_s, Y and W are exogenous.

Demand Equation: Order Condition

Let us examine the identification of the demand equation. First, we examine the order condition:

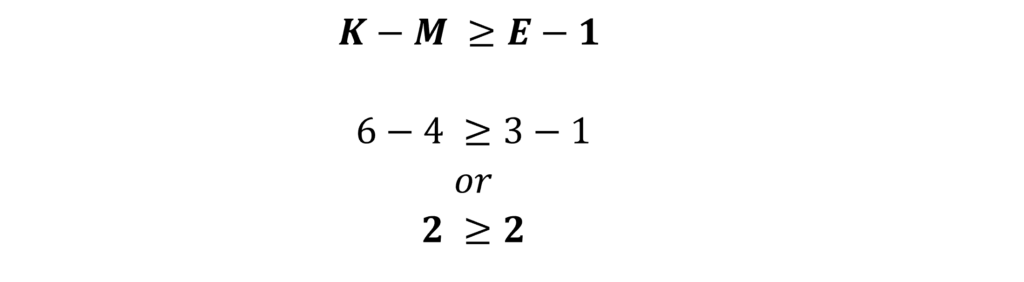
Therefore, the Order Condition is satisfied. Now, we move on to the Rank Condition of the demand equation.

Demand Equation: Rank Condition

To examine the rank condition, we need to form a matrix that includes coefficients of variables that are excluded from the demand equation. We rearrange the equations in the model to have all variables on the same side of the equation:

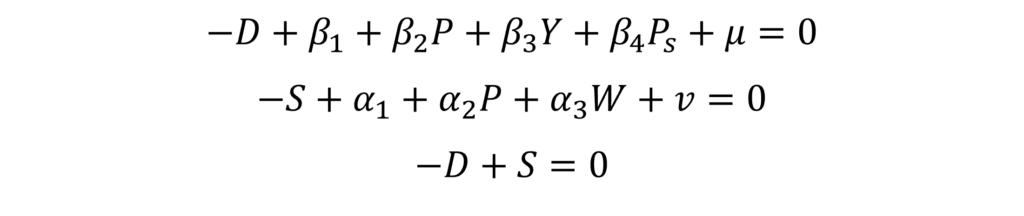
First, let us express all the variables in every equation in the form of a table:

	Variables
Equations	D	P	Y	P_s	S	W
Demand Equation	-1	B₂	B₃	B₄	0	0
Supply Equation	0	a₂	0	0	-1	a₃
Equilibrium Equation	-1	0	0	0	1	0

In this table, the zero values imply that the variable is not present in the equation. The values of other variables correspond to the coefficient of those variables.

From this table, we can construct the matrix required for the Rank Condition:

matrix for rank condition of identification

As we discussed, we need to form a matrix with coefficients of variables excluded from the equation, i.e. demand equation in this case. To do this, we strike out the entire demand equation from the table because those variables are included in the equation. And, we remove all the variables or coefficients that are present in the demand equation. Hence, we remove the first row and first to the fourth column to obtain the matrix of coefficients that are excluded from the demand equation and we end up with:

matrix determinant for rank condition of identification

Exactly-Identified or Overidentified

To check whether the demand equation is exactly identified or overidentified, we have to revisit the Order Condition:

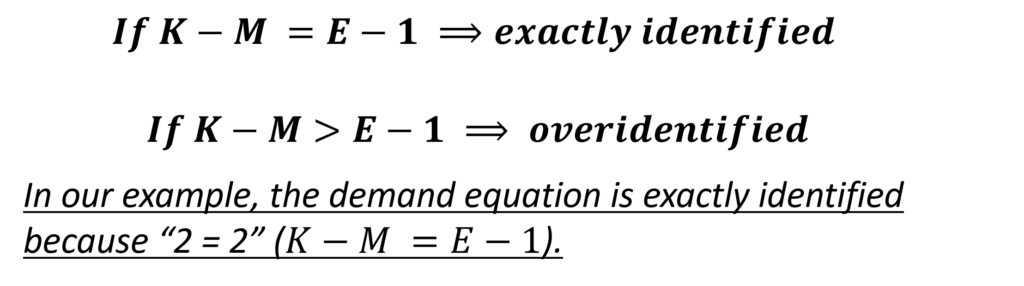
We can follow this same procedure to check the identification of the supply function as well, where we apply the Order Condition followed by the Rank Condition.

Note: the problem of identification may arise for equations that have coefficients to be estimated. We do not need to check the identification of equilibrium equations. For instance, the 3rd equation in the above example is an equilibrium equation (D = S). Therefore, we do not need to check the identification of such an equation.

Econometrics Tutorials