Blog

Multicollinearity refers to a situation where the independent or explanatory variables in the model have a strong relationship with each other. Perfect multicollinearity exists if the correlation coefficient for these independent variables is 1. Even if the problem of multicollinearity is imperfect, i.e. correlation coefficient is less than one, it can have serious consequences on the parameter estimates.

Consequences of Multicollinearity

• In the case of perfect multicollinearity, parameters or coefficients cannot be determined because the independent variables have a perfect correlation. In such a situation, the model cannot distinguish between the influence of given independent variables on the dependent variable. Therefore, their coefficients cannot be determined. In other words, the model fails to explain and separate the effect of each independent variable on the dependent variable.
• Imperfect multicollinearity also poses serious problems to the accuracy of econometric models. The parameter estimates or coefficients can be determined in the presence of less than perfect multicollinearity. But, the independent variables are still highly correlated, leading to large standard errors of coefficients. Hence, the estimated coefficients have low accuracy or precision.

Causes of Multicollinearity

Inherent in Economic Variables

Multicollinearity is inherent in economic variables because they tend to move in similar directions. For instance, consider the following consumption function:

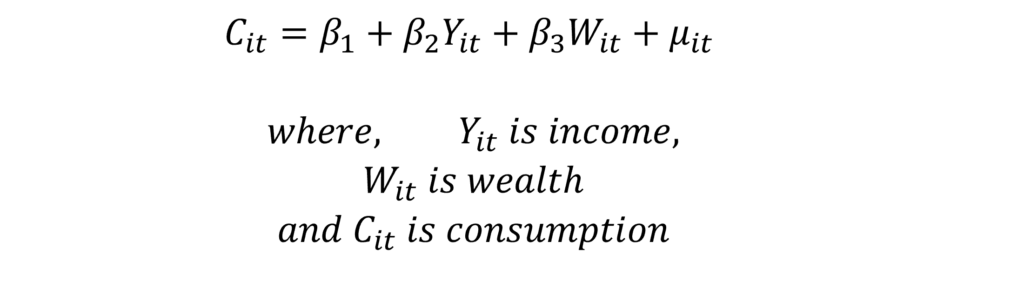
It is a common observation that the independent variables of income and wealth are highly correlated. Both these variables may increase or decrease together at somewhat the same rates, leading to the problem of multicollinearity. In cross-sectional studies, income and wealth move in a similar manner. High-income households or individuals also have high wealth or assets and vice versa.

Time Series Variables

In time series analysis, multicollinearity is a common problem because economic variables tend to have similar variations over time. For instance, economic variables like employment, income, consumption, savings and investment increase during periods of a boom in the economy. Similarly, they decrease during periods of slump or recession. As they tend to vary in a similar manner, the inclusion of these variables may result in multicollinearity in the model.

Inclusion of Lagged Variables

The use of lagged variables in econometric models can cause multicollinearity. For instance, a consumption function may include a lagged income variable. That is, consumption depends on current income as well as previous or past income.

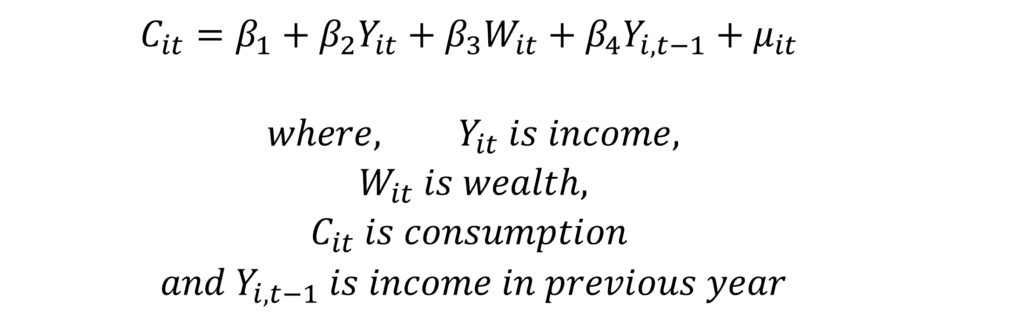
In the above model, income variable and lagged income will be highly correlated and cause multicollinearity. Hence, models with lagged variables tend to have a serious problem of multicollinearity.

detection of Multicollinearity

Variance Inflation Factor (VIF)

VIF or variance inflation factor is an estimate of the increase in variance of a coefficient due to the presence of multicollinearity. The existence of multicollinearity increases the standard errors, which is a measure of the standard deviation of a parameter estimate or coefficient. Therefore, VIF also shows whether the standard error of the coefficient is being inflated. The formula for calculating VIF is:

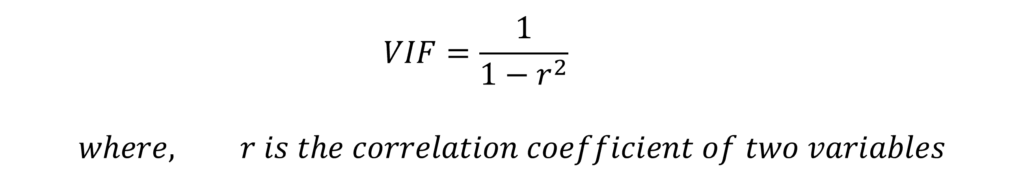
In a multivariate regression model, VIF for each independent variable is calculated as follows:

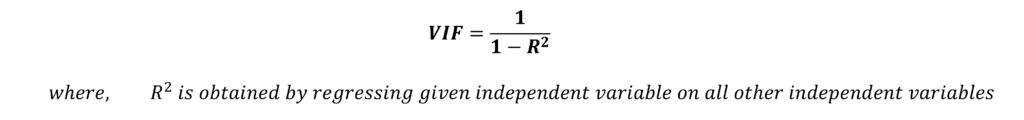
For instance, if a model has three different independent variables X₁, X₂ and X₃, then, the VIF of X₁ is calculated by running a regression with X₁ as the dependent variable, X₂ and X₃ as independent variables. The estimated R² from this regression is plugged into the VIF formula, which gives the value of VIF of X₁.

The value of VIF is always greater than 1 because R² cannot be negative in the usual OLS context. Generally, if the value of VIF is greater than 10, multicollinearity is considered a serious problem.

VIF > 10: Serious problem of Multicollinearity

Combination of Standard Errors, Correlation Coefficients and R²

Employing these measures together can help detect the presence of multicollinearity and its seriousness. These measures should be used in combination to ascertain whether multicollinearity is a serious problem. On their own, they are not enough to make certain conclusions about multicollinearity because:

• Large standard errors may be observed due to several reasons apart from multicollinearity. For instance, the standard error of a coefficient can be large simply if the variance of that independent variable is less.
• The correlation coefficient does not have to be necessarily high to have adverse effects on the estimates. Multicollinearity might be a problem even at moderately high correlations. Therefore, the correlation coefficient alone cannot be used to conclude the seriousness of multicollinearity.
• The R² can be high in the presence of multicollinearity, even when the coefficients are less precise.

Detection: Example

Let us consider the following model:

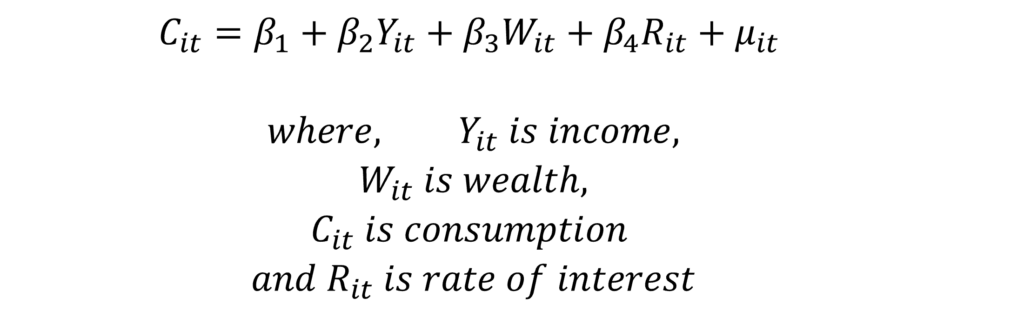
We can estimate this simple linear model using OLS and calculate the variance inflation factors (VIF) using any statistical software package:

Variable	VIF
Y (Income)	35.29
W (Wealth)	33.46
R (Rate of Interest)	1.46

The above results show that VIF is greater than 10 for income and wealth, which is a high value for VIF. Both these variables are the source of serious multicollinearity in the model. A high correlation between income and wealth is generally expected by economists because they tend to move in similar directions.

Using Correlation Coefficient, Standard Errors and R²

Correlation Coefficients	Y (Income)	W (Wealth)	R (Rate of Interest)
Y (Income)	1
W (Wealth)	0.98	1
R (Rate of Interest)	0.3	0.2	1

Here, the correlation between income and rate of interest is 0.3. The correlation between wealth and rate of interest is 0.2, i.e. correlation coefficient is low. However, the correlation between income and wealth is 0.98, which is close to unity. Such a high value of correlation can interfere with the accuracy of OLS. But, it is not enough to conclude that multicollinearity will be a serious problem in the precision of parameter estimates.

We know that income and wealth may be highly correlated from their economic relationship and tendency to vary together. Therefore, we can run separate regressions- one with both variables (income and wealth) in the model and the other with only one variable (income or wealth).

Consumption (C)			R-square = 0.6400	Adj. R-square = 0.6271
	Coefficient	Standard error	t	P-value
Income (Y)	0.799	0.1133893	7.06	0.000
Constant	-29.99	11.33948	-2.65	0.013

Consumption (C)			R-square = 0.4900	Adj. R-square = 0.4718
	Coefficient	Standard error	t	P-value
Wealth (W)	0.699	0.1349602	5.19	0.000
Constant	-89.99	26.99237	-3.33	0.002

Consumption (C)			R-square = 0.8182	Adj. R-square = 0.8047
	Coefficient	Standard error	t	P-value
Income (Y)	2.87876	0.4123721	6.98	0.000
Wealth (W)	-2.121183	0.4123719	-5.14	0.000
Constant	186.3606	42.85501	4.35	0.000

Interpretation

• A high correlation coefficient was observed between income and wealth.
• The variables are significant and R² is high in the model with both income and wealth. But, the standard errors have seen a huge increase. For income, the standard error increased from about 0.11 to 0.41 with the inclusion of wealth in the model. Similarly, the standard error for the wealth coefficient inflated from about 0.13 to 0.41 in the model including both income and wealth. Hence, the precision of estimates deteriorated a lot as the standard errors increased by almost 4 times.
• In the model including only wealth as an independent variable, there is a significant positive relationship between wealth and consumption. However, the coefficient associated with wealth becomes negative in the model including income and wealth. The sign of the wealth coefficient has changed, which is an indication that the results of the model are severely affected due to multicollinearity.
• Observing the R² can be misleading because its value increases to 0.8182 with both income and wealth included, but, the model is suffering from low precision as observed from changes in standard errors. Even the coefficients are significant as their P-value is less than 0.05. However, careful examination of standard errors and coefficient signs reveals that multicollinearity is a serious problem.

Solutions to Multicollinearity

Dropping the Variable

If multicollinearity is seriously affecting the results of the model, one of the solutions is to simply drop the variable causing the problem. This can be carried out in case of variables that are unimportant from the economic perspective. However, dropping important variables can undermine the model, for instance, wealth should not be removed from a consumption function because this leads to specification errors.

Do nothing

In some cases, multicollinearity is not a serious problem, i.e. the parameter estimates are not seriously affected. Some presence of multicollinearity can, therefore, be tolerated.

It is also possible that the overall results from the model are satisfactory. Even when multicollinearity does not allow accurate estimation of parameters separately, the overall effects of the variables are still captured by the model. If some of the variables are significant, those estimates can still be used for forecasting. Moreover, variables with multicollinearity can also be used for forecasting if the pattern of multicollinearity remains the same in the forecast period.

Transforming the Variables or using different estimation methods

In time series analysis, multicollinearity is a common problem because of the use of lagged variables. However, using different forms of these variables can eliminate this problem. For instance, instead of including lagged variables, it is common practice to employ first-difference or second-difference transformations of the variables.

In practice, time series analysis has several methods such as VAR, VECM, ARMA, ARIMA and other models that may be better suited for time series.

Generally, economic variables have intricate relationships with each other. It is possible to introduce new equations and variables in the model that make better economic sense and capture the relationships between different variables. Models with multiple equations can be estimated using simultaneous equation methods such as 2SLS, ILS and 3SLS.