The Wu-Hausman Test can be used to determine whether the Fixed Effects Model or Random Effects Model is more appropriate. To apply this test, we need to estimate both the Fixed Effects and Random Effects Models and compare the estimated coefficients using Wu-Hausman statistic.
To test whether the random effects are significant or not, the Lagrange Multiplier Test for Random Effects is often used.
Econometrics Tutorials with Certificates
Hypothesis
Before we state the hypothesis of the Wu-Hausman Test, we must discuss the meaning of consistency and efficiency of coefficients in brief.
Consistent estimates: coefficients of a model are said to be consistent if they keep getting closer to their true parameter values with an increase in sample size.
Efficient estimates: coefficients are said to be efficient if they have minimum variance as compared to the coefficients of other estimators. This means that the errors (difference between predicted and true values) are minimum in the case of efficient estimates, as compared to any other estimates.
The null and alternate hypothesis for this test can be stated as:

Under the null hypothesis, the coefficients of both the fixed effects and random effects models are consistent. However, only the coefficients of the random effects model are efficient. If we cannot reject the null hypothesis using the Wu-Hausman test, it means that the random-effects model should be preferred.
On the other hand, only the coefficients of the fixed effects model are consistent under the alternate hypothesis. The coefficients of the random effects model are not consistent. If we reject the null hypothesis, the fixed-effects model should be preferred instead of a random-effects model.
Estimating the Wu-Hausman Test statistic
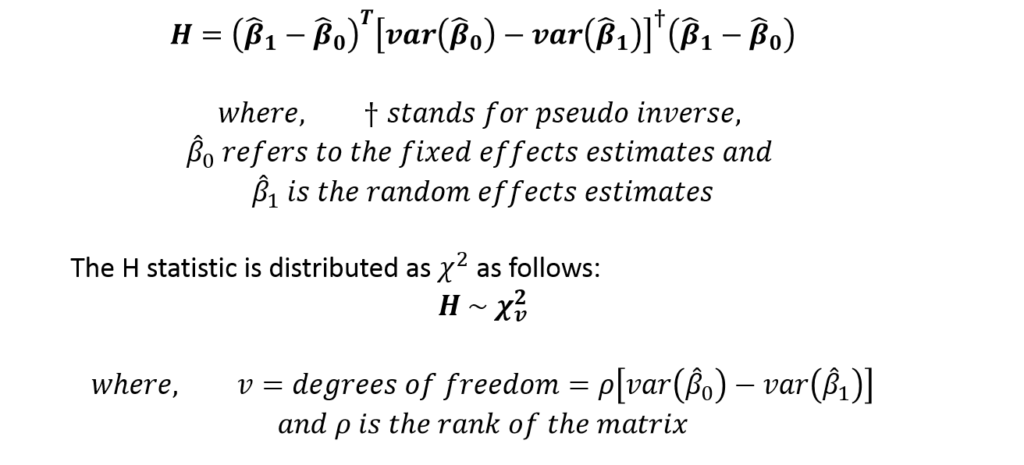
The statistic can be estimated using statistical software packages.
If H is greater than the critical chi-square value, the null hypothesis is rejected. We conclude that Fixed Effects estimates are consistent. Whereas, Random Effects estimates are not consistent. Hence, the Fixed Effects Model should be used.
If H is less than the critical chi-square value, we cannot reject the null hypothesis. Both Fixed and Random Effects models are consistent. However, Random Effects estimates are efficient as well. Hence, the Random Effects Model is more reliable.
Interpretation in practice
In practice, the results of the Wu-Hausman test look like the following:
| Independent variable | Coefficients of Fixed Effects Model | Coefficients of Random Effects Model |
| X | -0.013 | -0.012 |
| Y | 0.047 | 0.039 |
| H = 3.26 | ||
| P-value = 0.1963 |
Hence, the results of the above table indicate that the H = 3.26. Using the P-value reported above, we cannot reject the null hypothesis. This means that the coefficients of the random-effects model are consistent as well as efficient. Hence, we should apply the random-effects model.
Econometrics Tutorials with Certificates
This website contains affiliate links. When you make a purchase through these links, we may earn a commission at no additional cost to you.



