We already discussed the Production Possibility Curve associated with two outputs and the Economies of Scope. Here, we will analyze how a multi-product firm can achieve equilibrium. It can help the forms decide the quantity of each product, given their limited inputs.
Econometrics Tutorials with Certificates
equilibrium of a multi-product firm
We will consider a firm that makes two products- X and Y. Given the labour and capital that the firm employs, the choice of allocation of these inputs to produce two outputs (X and Y) becomes essential. This multi-product firm will be in equilibrium with the efficient allocation of inputs between the two products. That is, the firm needs to choose the quantity of labour and capital to be allocated to each product.
Both the products, X and Y, have different isoquants. The total labour and capital that the firm uses are fixed. More inputs diverted to one product will reduce the inputs available for the other product. Therefore, if the production of one product increases and its isoquant shifts towards higher output, the output of other product will have to be reduced.
Using the Edgeworth-Box Diagram
In the diagram, the origin for product X and its isoquants are shown by OX in the bottom left corner. On the other hand, the origin of product Y and its isoquants is on the opposite side, i.e. top right corner at OY. The X-axis shows the labour used and Y-axis shows the quantity of capital. In this way, we can show the isoquants and input allocation for both the products together, with fixed total inputs of labour and capital.
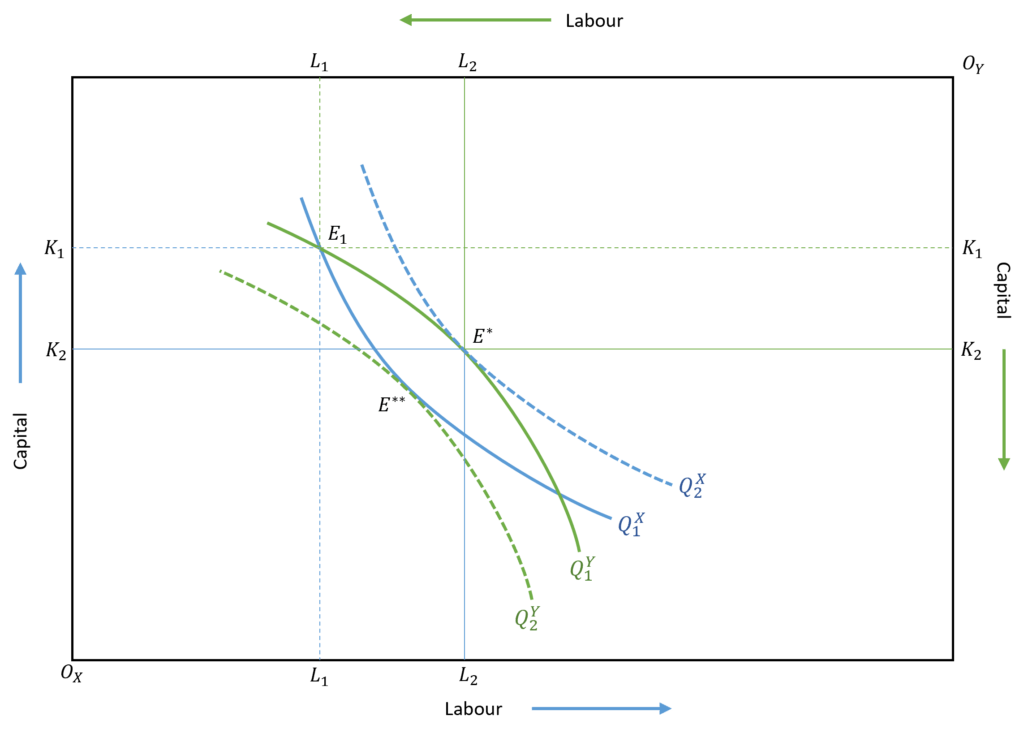
A multi-product firm will achieve equilibrium at the tangency of isoquants of both the products because the firm will maximize the output of both X and Y with the given inputs.
Efficient allocation
Let us consider a point away from the tangency of isoquants. At point E1, the firm will produce Q1Y quantity of product Y and Q1X quantity of product X as shown by the isoquants of both the products. The isoquants are not tangent, but, intersect each other at this point. The allocation of labour and capital is such that the firm will allocate OXL1 labour and OXK1 capital to product X. The remaining labour (OYL1) and remaining capital (OYK1) is used to produce Y.
However, this allocation is inefficient because the firm can increase the output of X or Y by simply reallocating the inputs. The firm can move to a higher isoquant without increasing inputs and input costs. This equilibrium is achieved at points E* and E**. Let us consider point E* for example, where the isoquants Q1Y and Q2X are tangent.
By shifting to this point, the firm will be able to increase the output of X by moving to a higher isoquant from Q1X to Q2X. Higher isoquant means higher output, therefore, the firm is able to increase the output of X while the output of product Y is still the same at Q1Y.
Different points of efficient allocation
Hence, the firm achieves an efficient allocation of inputs at E*. Here, the firm uses OXL2 labour and OXK2 capital in the production of X. The remaining inputs, OYL2 labour and OYK2 capital are used to produce Y.
Similar to E*, the firm can also choose to operate at E** to achieve efficient allocation. The difference between the two is that the firm will move to a higher isoquant Q2Y and produce more of Y, while the output of product X will remain the same.
These points are efficient and determine the equilibrium of a multi-product firm with the given level of inputs. The only way to increase the output of either X or Y or both is to increase the total inputs of labour and capital.
Production contract curve
In the previous section, we observed that a multi-product firm can produce efficiently by allocating inputs based on the tangency of isoquants at points E* and E**. This shows that there can be more than one point of tangency or equilibrium. This will depend on the quantity of both outputs (products X and Y). At each point of equilibrium, the combination of outputs is different.
The production contract curve shows all these points of equilibrium, where different isoquants of products X and Y are tangent. Hence, all the points on the production contract curve lead to efficient production. The firm will choose to operate on this curve depending on the combination of quantity of X and Y they wish to produce. The combination of output of each product will, therefore, determine the amount of labour and capital allocated to them.
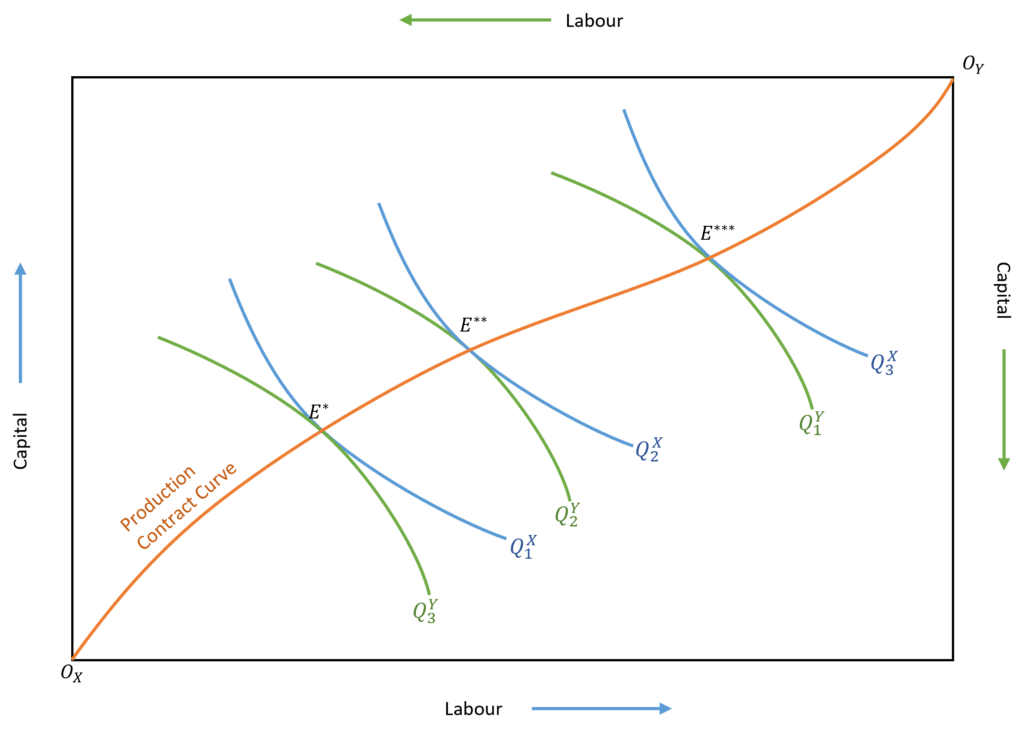
Finally, this Edgeworth-Box diagram shows the production contract curve. Hence, all the points on the curve (including E*, E** and E***) depict the tangency of all possible isoquants of X and Y. Every point on this curve leads to an efficient allocation of inputs. Based on the quantity of X and Y that the firm wants to produce, it will choose to operate on one of the points on the curve. This will, therefore, determine the allocation of labour and capital to each product.
Econometrics Tutorials with Certificates
This website contains affiliate links. When you make a purchase through these links, we may earn a commission at no additional cost to you.


