The R square and Adjusted R square are often used to assess the fit of the Ordinary Least Squares model. These measures, therefore, help ascertain how well the estimated model accounts for the variations in the dependent variable. Furthermore, they can help in determining the importance of independent variables in the model. They can also assist in removing any unnecessary independent variables.
Econometrics Tutorials with Certificates
R square
The R square is the estimate of the proportion of total variation in the dependent variable that is explained by the independent variables in the model. Additionally, it is sometimes referred to as the coefficient of determination. The R square for a model can be estimated using the following formula:

Total Sum of Squares
TSS or Total Sum of Squares represents the total variations in actual values of the dependent variable (Y) from the sample mean value. Hence, it can be calculated by squaring the deviation of each value of actual Y from the mean of actual Y and adding up all the deviations. That is, it can be estimated as:
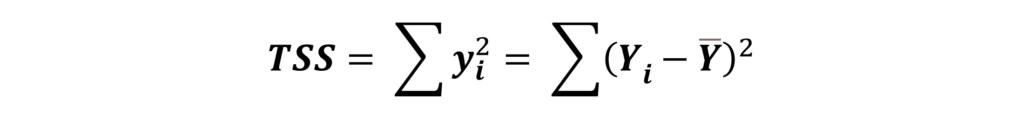
Explained Sum of Squares
ESS or Explained Sum of Squares is the total variations in the estimated values of the dependent variable (estimated using OLS) from the sample mean value. Hence, it is calculated as the sum of squared deviations of each predicted value of the dependent variable from the mean of actual Y. Therefore, it can be calculated as:

Residual Sum of Squares
Residuals are the deviations of the predicted or estimated dependent variable from the actual value of dependent variable Y. RSS or Residual Sum of Squares is calculated by further squaring the sum of these deviations or residuals and is obtained as:
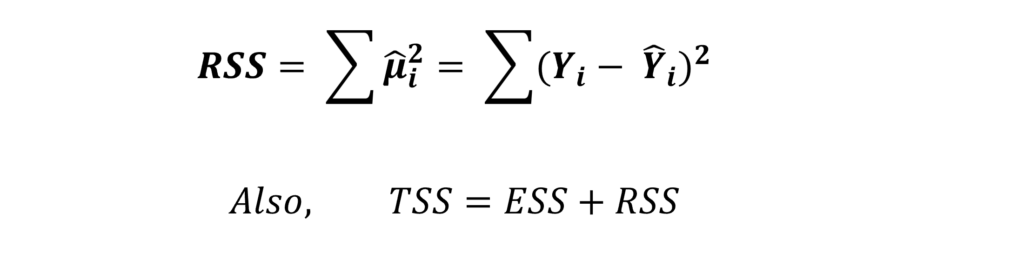
Moreover, Total variations in the dependent variable (TSS) are a sum of the explained variations in the model (ESS) and residual variations (RSS). Hence, the square of explained variations will always be less than the square of total variations in the dependent variables.
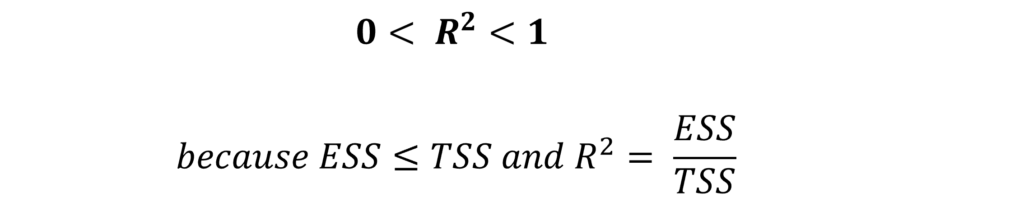
If R square = 1, then it means that ESS = TSS. The model is a perfect fit because independent variables explain all the variations in the dependent variable.
If R square = 0, it implies that there is no relationship between the dependent variable (Y) and the independent variables. Moreover, in such a case, all coefficients associated with independent variables will be zero.
Generally, the value of R square lies somewhere between 0 and 1. The closer its value is to 1, the better the fit of the OLS model. Hence, it is desirable to have higher values of R square which are closer to 1.
Drawbacks of R Square
Finally, a major drawback of the R square estimate is that its value can be easily increased by including more independent variables. By adding more independent variables to the model, the explained variations can only increase. That is, it will never decrease even if the variables are unnecessary. Therefore, a higher value of R square can be easily achieved because it does not consider the impact of including unnecessary variables.
Econometrics Tutorials with Certificates
This website contains affiliate links. When you make a purchase through these links, we may earn a commission at no additional cost to you.


