Interpretation of Coefficients: OLS

The OLS or Ordinary Least Squares is one of the most widely used models in Econometrics and many other fields. Therefore, the interpretation of coefficients is one of the most critical aspects of its application. Even in the case of many other models, the interpretation of coefficients is similar to that of OLS. Here, we will continue with the same hypothetical data used in Ordinary Least Squares Estimation to illustrate the interpretation of the results of the OLS model.

Econometrics Tutorials

Variables in their original form

When the variables are in their original form, our model can be expressed as follows:

In the model above, all the variables are used in their original form. That is, Quantity demanded is expressed in units of commodity and independent variables of price, price of substitute and income are in monetary units.

Hence, the result of this model can be easily obtained by applying OLS using any statistical software:

Quantity demanded (y)

	Coefficient	Standard error	t	P-value
Price (p)	-2.004936	0.2764868	-7.25	0.000
Price of substitute (x)	0.7060227	0.1753896	4.03	0.007
Income per capita (i)	0.3263422	0.0272013	12.00	0.000
Constant	27.03021	26.28797	1.03	0.343

In this model, the coefficients can also be interpreted in terms of units. Moreover, we know that the dependent variable of quantity demanded (y) is determined by its price (p), price of the substitute good (x) and income of consumers (i). All the coefficients (except the constant) are statistically significant because their p-values are less than 0.05, the t-values are greater than the critical t-values and the standard errors are also small in comparison to the coefficients.

Relationship with Price (p)

The coefficient associated with price (p) B₂ which is equal to -2.004936. The negative sign of the coefficient suggests a negative relationship between the price of the commodity and its quantity demanded. That is, the quantity demanded of that commodity falls with a rise in its price.

Based on the value of the coefficient, the quantity demanded falls by about 2 units (-2.004936) with a 1 unit rise in price. If the price is in dollars, we can say that a 1 dollar increase in price leads to an approximately 2 units decrease in quantity demanded. This relationship, therefore, adheres to the law of demand in this case.

Relationship with Price of Substitute (x)

Here, the positive coefficient value indicates a positive relationship. This implies that with a rise in the price of the substitute, the quantity demanded of this commodity increases. With a 1 unit (or 1 dollar) increase in the price of the substitute good, the quantity demanded of the commodity also increases by approximately 0.7 units (B₃ = 0.7060227).

As the price of the other good (x) increases, commodity ‘y’ becomes relatively cheaper. Therefore, consumers start buying more of ‘y’ and its quantity demanded increases. Moreover, this relationship confirms that good ‘y’ and good ‘x’ are substitutes, not complementary goods.

Relationship with Income (i)

With a 1 unit (or 1 dollar) increase in income, the quantity demanded increases by approximately 0.3 units (B₄ = 0.3263422). This further indicates that commodity ‘y’ is most likely a normal good as its quantity demanded increases with an increase in the purchasing power of consumers.

Significance of the Constant

Here, we do not care about the significance and value of the constant. The Quantity demanded of ‘y’ will be equal to the value of the constant (B₁ = 27.03021) when all the independent variables are equal to zero. In this example, the value of zero for all the independent variables is an impossible scenario. This is because the price (p), price of substitute (x) and income per capita (i) will never be zero in reality.

Note: the value of the constant can also be important in some situations. For instance, the constant is an important coefficient in a Keynesian consumption function. It tells us about the minimum or necessary consumption expenditure of consumers in a situation where income falls to zero.

Log-log transformation and interpretation of coefficients

In this model, all the variables, i.e. dependent as well as all independent variables are log-transformed before estimating with OLS. Such a transformation is especially useful in economics and often preferred. This is because the coefficients in such a model represent the approximate elasticity of the dependent variable with respect to independent variables.

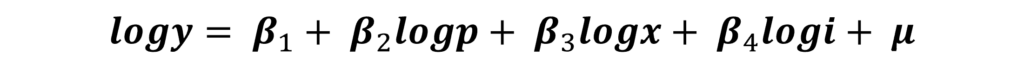
This model can be easily estimated by log transforming all the variables before applying OLS in any statistical software.

Log of Quantity demanded (logy)

	Coefficient	Standard error	t	P-value
Log of Price (logp)	-0.3209715	0.0431188	-7.44	0.000
Log of Price of substitute (logx)	0.1628261	0.0392135	4.15	0.006
Log of Income per capita (logi)	1.03102	0.0872347	11.82	0.000
Constant	-0.8539467	0.6084275	-1.40	0.210

Similar to the previous regression, all the coefficients are statistically significant. However, the interpretation of these coefficients is in terms of elasticity.

Price Elasticity of Demand

The coefficient of “logp” represents the price elasticity of demand of good ‘y’. Moreover, the negative sign on the coefficient means a negative relationship between price and quantity demanded. Other variables being constant, with a 1 per cent increase in the price of ‘y’, the quantity demanded of commodity ‘y’ decreases by approximately 0.32 per cent (B₂ = -0.3209715). This relationship also follows the law of demand. Since the approximate price elasticity is less than 1, commodity ‘y’ is most likely a necessity because necessary goods tend to have lower price elasticity.

Cross Elasticity

Furthermore, the coefficient associated with “logx” represents the cross elasticity of demand of good ‘y’ with respect to good ‘x’. If we hold other variables constant, with a 1 per cent increase in the price of ‘x’, the quantity demanded of commodity ‘y’ increases by approximately 0.16 per cent (B₃ = 0.1628261). Because there is a positive relationship between the two, we can conclude that goods ‘y’ and ‘x’ are substitutes. If they were complementary goods, we would see an opposite relationship where the quantity demanded of ‘y’ would fall with a rise in the price of ‘x’.

Income Elasticity

We can observe a positive income elasticity in the case of good ‘y’ because of the positive sign of the coefficient. Holding other variables constant, the quantity demanded of ‘y’ increases by approximately 1.03 per cent (B₄ = 1.03102) with a 1 per cent increase in income. Hence, income elasticity is almost unitary elastic. Additionally, commodity ‘y’ is most likely a normal good because its demand increases with an increase in income.

Econometrics Tutorials