Ordinary Least Squares Estimation

OLS or Ordinary Least Squares is one of the most common methods used in Econometrics. It is a linear regression technique that minimizes the sum of squared residuals (error term) to estimate the coefficients. In this post, we will dive further into the practical process of estimating the coefficients using Ordinary Least Squares.

Econometrics Tutorials with Certificates

The Ordinary Least Squares Equation

Suppose, we need to estimate the quantity demanded of a commodity ‘y’. According to economic theory, demand for any commodity depends on several factors such as its price, the price of other commodities, income, etc. For illustration purposes, we will also use three variables representing the price of y (denoted by ‘p’), the price of a substitute good (x) and income (i). In such a situation, therefore, the quantity demanded of y is the dependent variable. Its price, price of substitute good “x” and income (i) are independent or explanatory variables. Each observation of quantity demanded (y) can also be written in equation form as follows:

Moreover, for different combinations of independent variables, the data has a corresponding value of ‘y’. For instance, if there are 50 observations, then we have 50 different values of ‘y’ corresponding to 50 different combinations of independent variables’ values.

OLS: The Matrix Form and Normal Equation Estimation

Generally, OLS estimation is carried out using matrices. The above equation can also be expressed in the form of matrices as follows:

Furthermore, the first column of X includes all values of 1 because of the constant. That is, it does not have any independent variable attached to it. Therefore, this column is necessary to estimate the constant.

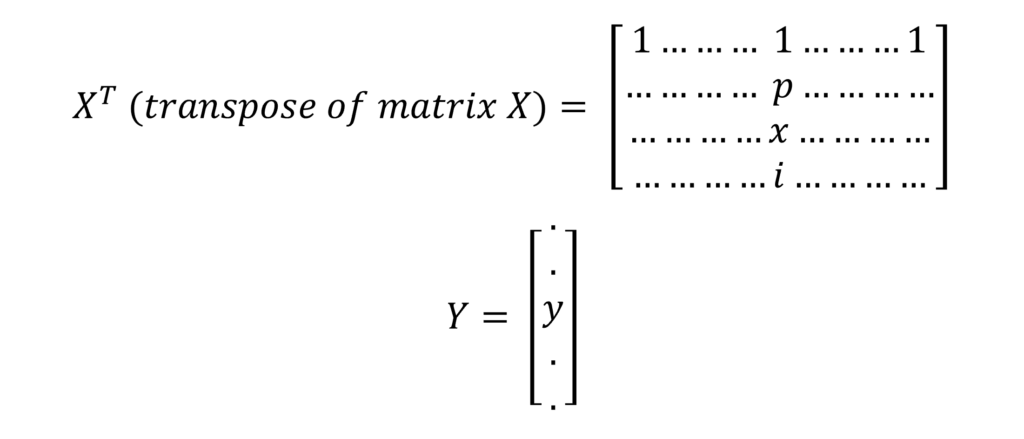
Hence, the values of coefficients can be estimated using matrix multiplications, transpose and matrix inverse calculations. Further, this can be easily accomplished using any econometric software package.

Estimation with real data

To demonstrate, we will consider a small hypothetical data sample of 10 observations for the variables used above.

Observations	Quantity demanded of commodity ‘y’	Price of ‘y’ (p)	Price of substitute good ‘x’	Income (i)
1	232	47	49	811
2	247	35	62	769
3	290	38	63	906
4	246	42	65	803
5	239	43	64	761
6	265	33	69	774
7	245	44	60	814
8	227	36	47	735
9	237	46	68	775
10	273	37	53	853

The quantity demanded ‘y’ can be predicted from any given values of independent variables and their coefficients. This is accomplished by further substituting values in the following equation:

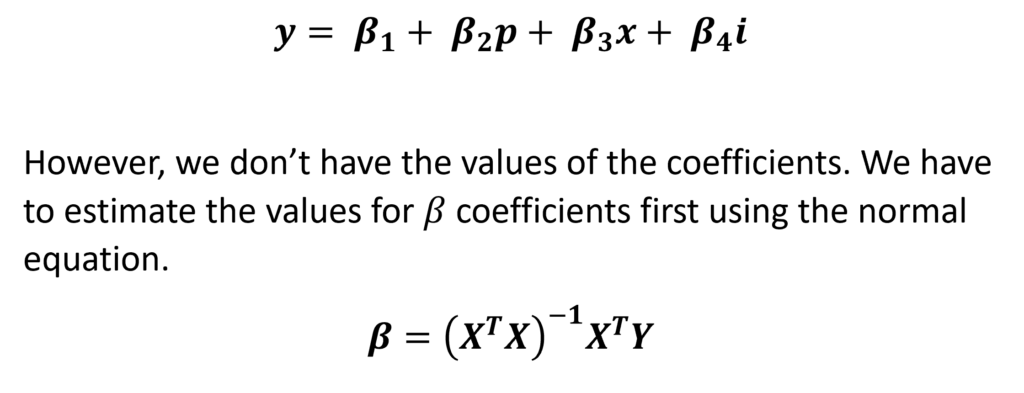
From the given data, we can also construct the matrices to estimate the coefficients with the normal equation method. Hence, the matrices for the above equation can be constructed as follows:

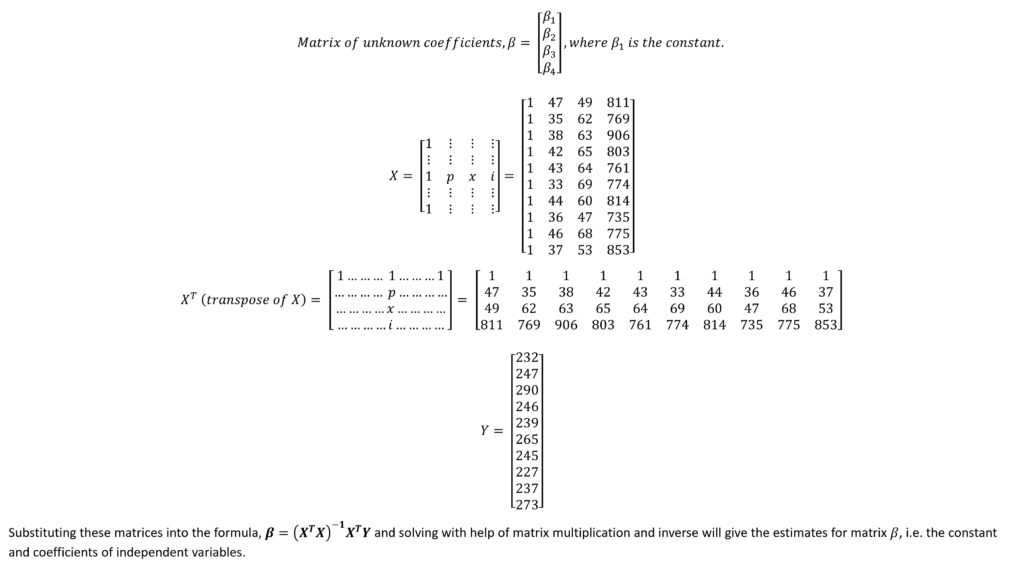
On solving, the values of coefficients based on the given data were estimated as:

Making predictions after ordinary least squares

Suppose, we also have to predict the quantity demanded of commodity ‘y’, given values of independent variables as p = 42, x = 57 and i = 780. Then, we can forecast ‘y’ using the OLS equation:

Hence, this means that the quantity demanded of “y” will be 241 at the given price of 42, the price of substitute “x” at 57 and the income of 780.

Estimating the residuals or error terms

The residuals or error terms are further estimated by subtracting the “predicted values of Y” from the “actual values of Y” for every observation. Therefore, they can be expressed as:

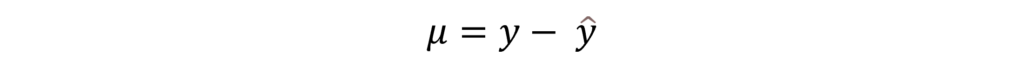
For each observation, we can also obtain the predicted values with the help of estimated coefficients and the values of independent variables from those observations. Then, we can estimate the residuals from the actual and predicted values.

Observations	Quantity demanded of commodity ‘y’	Price of ‘y’ (p)	Price of substitute good ‘x’	Income (i)	Predicted ‘y’ (using coefficients)	Residuals or error (y – predicted y)
1	232	47	49	811	232	0
2	247	35	62	769	252	-5
3	290	38	63	906	291	-1
4	246	42	65	803	251	-5
5	239	43	64	761	234	5
6	265	33	69	774	262	3
7	245	44	60	814	247	-2
8	227	36	47	735	228	-1
9	237	46	68	775	236	1
10	273	37	53	853	269	4

Note: predicted ‘y’ has been further rounded off to the nearest integer values here. The quantity demanded of a commodity is generally a whole number because consumers cannot buy fractions of a commodity in most cases. For example, a consumer cannot buy 0.3 units of a book.

Econometrics Tutorials with Certificates