The Breusch-Pagan Lagrange Multiplier Test is used to determine whether random effects are significant in panel data models. On the other hand, the Hausman Test is used to choose between fixed and random effects models. Both these tests are used extensively with panel data.
The Random Effects Model is also known as the Error Components Model or the two-error structure approach. The Fixed Effects Model with LSDV approach has some clear problems in the use of dummy variables. Moreover, the Fixed Effects ‘Within’ Model and LSDV model cannot include time-invariant variables. Hence, the Random Effects Model provides a different approach to account for cross-sectional and time-specific effects in panel data.
Instead of using dummy variables like in fixed-effects LSDV models, the cross-sectional and time-specific effects are included as error terms in the Random Effects Model.
Econometrics Tutorials with Certificates
Specification of Random Effects Model
A random-effects model including cross-sectional effects can be specified as follows:
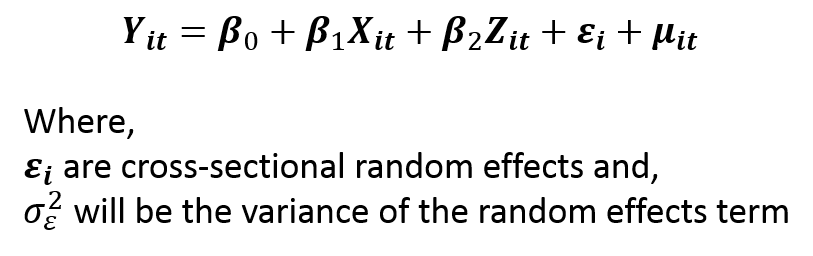
The random-effects term is not directly observable. However, we can obtain a joint distribution for both the error terms which is used to estimate the model with the Maximum Likelihood approach. Apart from this, the model can also be estimated using Generalized Least Squares (GLS). We will not go into its details in this post.
Lagrange Multiplier Test
The null hypothesis of the test can be stated as follows:
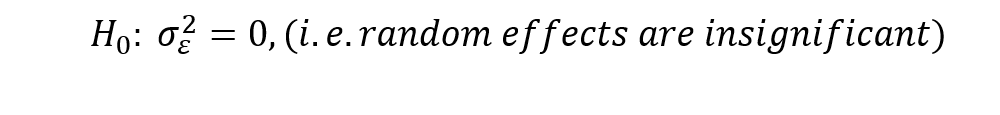
The test statistic can be estimated as:
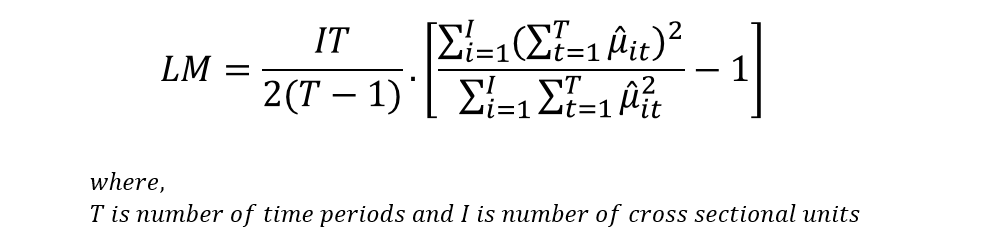
This LM statistic follows a chi-square distribution with 1 degree of freedom because we are testing for one measure only (variance of random effects term). If we reject the null hypothesis using this test, we conclude that the random effects are significant in the model and the use of the Random Effects Model is appropriate.
The Breusch-Pagan Lagrange Multiplier test is applied after estimating the Random Effects Model. The model and the test can be applied using statistical software packages. The results of the model show the variance of the error terms, chi-square value and p-value:
| Lagrange Multiplier Test for Random Effects | ||
| Variance | Standard deviation | |
| Dependent variable | 0.142 | 0.377 |
| Usual Error term | 0.072 | 0.268 |
| Random Effects term | 0.06 | 0.244 |
| Chi(1) = 3.98 | ||
| P-value = 0.023 |
In the above table, we reject the null hypothesis because the p-value is less than 0.05. We can also conclude that the Random Effects are significant. Hence, the use of the Random Effects model is appropriate.
Econometrics Tutorials with Certificates
This website contains affiliate links. When you make a purchase through these links, we may earn a commission at no additional cost to you.



