ADF Test: Augmented Dickey Fuller Equation

The Augmented Dickey Fuller or ADF Test of stationarity is a unit root based test. It attempts to overcome the shortcomings of the original Dickey Fuller test. Researchers often observed that the Dickey Fuller test equation suffers from autocorrelated error terms. As a result, Dickey and Fuller augmented their equation to address this problem. Hence, this updated version is known as the Augmented Dickey Fuller or ADF test.

Econometrics Tutorials

ADF test equation

Dickey and Fuller amended their equation to remove the autocorrelation of error terms. As a result, they augmented their model to include autoregressive terms of the dependent variable (∆Y_t) as follows:

The error term μ_t in this augmented model is a white noise error term and is not autocorrelated.

The remaining procedure is the same as the original Dickey-Fuller regression. The null hypothesis of α=0 is tested against the alternate hypothesis of α<0 using the Tau statistic. Moreover, it is estimated with the same formula as before.

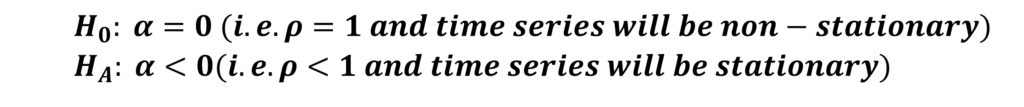
Similar to the original Dickey Fuller test, the coefficient “α” should be negative and significant for the time series to be stationary.

Choosing the number of lags of autoregressive terms

The number of lags or autoregressive terms (k) to include in the Augmented Dickey-Fuller model are determined in such a manner so that the error term is not serially correlated or autocorrelated. Furthermore, the Akaike or Schwarz Information Criteria is generally used to decide the appropriate lag length (k) in practice.

Application of ADF test with drift and trend

As in the case of the original Dickey-Fuller Model, the ADF test should also be applied to three different equations:

Including drift as well as trend
Including only drift
Without both drift and trend

Step 1: ADF test with drift and trend

Firstly, we use the ADF test on the time series to check whether it is stationary at level. From the three equations, we start with the equation including both trend and drift:

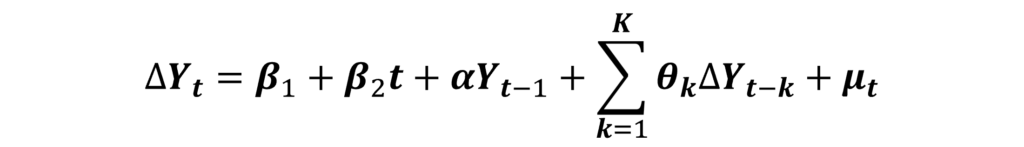
In this model, if the coefficient of trend (β₂) is significant, then, we use this model or equation to determine stationarity. Hence, we apply the Tau statistic to determine whether the coefficient “α” (associated with Y_t-1) is statistically significant or not. If this “α” is negative and significant, we conclude that the series is stationary at level. If this coefficient is either positive or insignificant, then the series is non-stationary at level.

However, if the coefficient of trend (β₂) is insignificant, we never apply the test of stationarity using the Tau statistic. Instead, we move on to the second equation including only the drift component.

Step 2: ADF test with only drift

Hence, we apply the ADF test to the equation with only drift when the trend is insignificant.

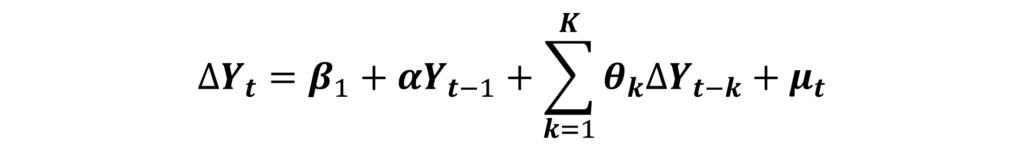
In this equation, if the drift component (β₁) is significant, we apply the test of stationarity using the Tau statistic. If the coefficient “α” (associated with Y_t-1) is negative and significant, we conclude that the time series is stationary at level. In case the coefficient is positive or insignificant, then the time series is non-stationary at level.

If the drift component (β₁) is insignificant, we do not need to apply the stationarity test to this equation. Hence, we move on to the next equation without drift and trend.

Step 3: ADF test without drift and trend

Therefore, we have to drop both the drift and trend components if they are insignificant. We use the following equation:

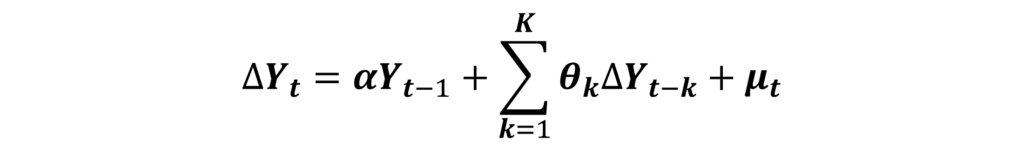
If we observe that the coefficient “α” (associated with Y_t-1) is negative and significant after applying the Tau-statistic, we conclude that the series is stationary at level.

Note: It is also possible that the time series is non-stationary at level. That is, the coefficient “α” is either positive or insignificant in the above procedure. If this happens, we further apply these tests on the time series at first difference.

Adapting the test to higher-order differences

If we observe that the time series is non-stationary at level, the next step is to determine whether the time series is stationary at first difference. The above equations only test the stationarity of the time series at level. Moreover, it is a common experience that the series is non-stationary at levels. In such cases, we can transform the time series by taking its first difference. To test this first difference form of the series, we have to further adapt the ADF test equations as well.

The three equations of the ADF test will be adjusted using the first difference form, and can be expressed as follows:

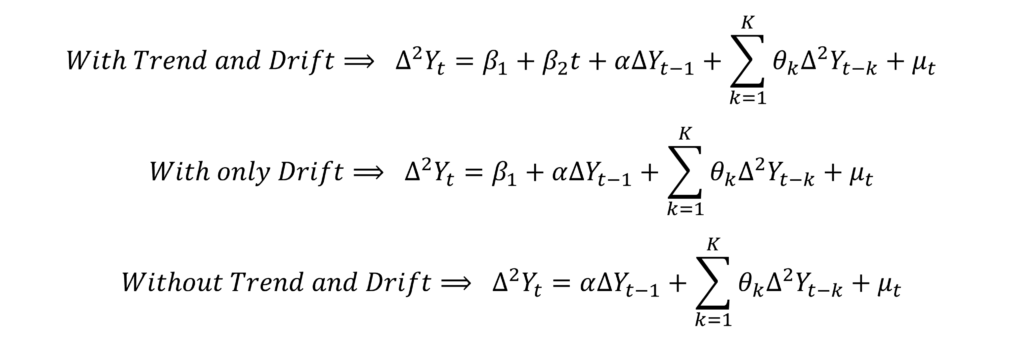
Here, our dependent variable has changed from “∆Y_t” to a new variable “∆²Y_t” after taking the first difference of the original series. Additionally, the variable associated with the coefficient “α” has also changed to the first difference form (from “Y_t” to a new variable “∆Y_t”). This is also true for all the autoregressive terms in the model.

Stationarity at First Difference

The testing procedure stays unchanged. Therefore, we apply the ADF test to the equation with the trend and drift first. If the trend is significant, we apply the Tau statistic to determine stationarity. The time series is stationary at first difference when coefficient “α” is negative and significant. If the trend is insignificant, we move on to the second equation with only drift and so on.

If coefficient “α” is negative and significant in this procedure, it means that the time series is stationary at the first difference. It is still possible that the coefficient is positive or insignificant in these equations. Then, the time series will be non-stationary at first difference. Finally, we will have to take the second difference and repeat the same procedure again.

Econometrics Tutorials