Information Criteria are used to compare and choose among different models with the same dependent variable. Akaike Information Criterion (AIC) and Schwarz or Bayesian Information Criterion (SIC or BIC) are most commonly used for model selection. Moreover, these criteria help measure how well the models fit the given data.
Econometrics Tutorials with Certificates
Information Criteria v/s R-square and Adjusted R-square
Akaike and Schwarz Information Criteria overcome the drawbacks associated with R-square and Adjusted R-square. The value of the R-square can be increased by including more independent variables in a model, even when the variables are unnecessary. Both these information criteria impose a penalty for including unnecessary independent variables. This means that information criteria are better in terms of determining the fit of a model and comparing different models. Information criteria can, therefore, be used to determine and drop unnecessary independent variables.
Moreover, R-square and Adjusted R-square should be used only for in-sample goodness of fit. They generally do not perform well in the case of out-of-sample observations. This implies that these measures should only be used as the goodness of fit measures for observations that were included in the model. For out-of-sample forecasting or observations that were not used in training the model, these measures are not reliable. Information criteria (AIC and SIC/BIC), on the other hand, can be used as the goodness of fit measures for out-of-sample observations as well.
Estimation of Information Criteria

While comparing different models, the model with the lowest value of AIC and SIC (or BIC) is preferred because the greater the number of unnecessary parameters, the higher the value of AIC/SIC due to the penalty. Finally, the model with the lowest value of Information Criteria is considered to be a better fit for the given data.
Examples
Choice of autoregressive and moving average terms in ARIMA
Information Criteria can be used to choose the number of lags to include in a model. In ARIMA and ARMA models, one of the most important steps in estimation is to choose the appropriate number of autoregressive and moving average terms. To learn further about the ARIMA models, go to ARIMA Estimation and Model Selection.
Here, we will compare the Information Criteria for ARIMA(1,0,1), ARIMA(2,0,2) and ARIMA(1,0,0) and their results. Also, we must estimate each ARIMA model and the Information Criteria for each model. Finally after comparison, we choose the model with the lowest value of AIC or SIC for further analysis such as forecasting.
| Model | AIC | SIC/BIC |
| ARIMA (1, 0, 1) | -341.2521 | -328.3933 |
| ARIMA (1, 0, 0) | -341.5068 | -330.7912 |
| ARIMA (2, 0, 2) | -337.4508 | -320.3058 |
In practice, we may have to estimate more combinations of autoregressive and moving average terms. From the above models, ARIMA(1, 0, 0) performs better than the other models because the value of both AIC (-341.5068) and SIC (-330.7912) is the lowest for it. Hence, we should include one autoregressive term and no moving average terms. The time series was stationary at level, therefore, it was integrated of order 0. We conclude that ARIMA (1, 0, 0) is a better fit.
VAR Models
In the Vector Autoregressive or VAR model, all variables are considered endogenous variables. The number of equations in VAR is also equal to the number of variables. Moreover, each variable is treated as the dependent variable in one equation. The independent variables include the lags of all the variables in the model. For example, a VAR model of order 2 (or 2 lags) will contain 2 lags of every variable as independent variables in each equation and can be specified as:
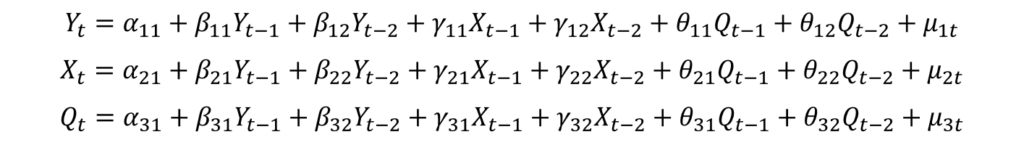
The above VAR model consists of 3 endogenous variables (X, Y and Q) and each variable is the dependent variable in one equation. Because this is VAR of order 2, each equation has 2 lags of all variables as the independent variables.
Choice of lags in VAR models
However, it may not be possible to know the appropriate number of lags beforehand. Therefore, we must determine the order of the VAR model or the number of lags that must be used in VAR. For this purpose, we use Information Criteria. It is important to note that the general formulas for AIC and SIC have to be slightly adjusted for multivariate models such as the VAR and VECM Models (learn more). Let us look at the results:
| VAR Lag Order | AIC | SIC/BIC |
| 1 | -11.5741 | -11.1516 |
| 2 | -11.4628 | -10.7234 |
| 3 | -11.2321 | -10.1747 |
| 4 | -11.2847 | -9.9114 |
Based on the results of the Information Criteria, we can conclude that the VAR model of Order 1 or Lag 1 is appropriate. This is because it has the lowest values of AIC (-11.5741) and SIC (-11.1516) among all the models.
In addition to the above examples and choosing among models, Information Criteria are used in many other instances such as choosing the lag order under the Augmented Dickey-Fuller test of stationarity.
Econometrics Tutorials with Certificates
This website contains affiliate links. When you make a purchase through these links, we may earn a commission at no additional cost to you.



In the “choice of lags in VAR” example what would be the k parameter in the AIC and BIC equation?
Is k = (number of endogenous variables)*(number of lags)+1
In the “choice of lags in VAR” example what is the value of the k parameter in the AIC/BIC formulas?
Is k = (endogenous variables +1 )*(number of lags)
In the case of VAR models, the AIC and BIC formulas are adjusted a little and sometimes estimated using Log-likelihood. There are different versions of formulas that are available for this. Generally, we use the formulas advised by Lutkepohl. In those, we use “pK^2” in AIC and BIC, where K = number of endogenous variables and p = lag order of VAR.
You can find the complete formulas here:
Lütkepohl, H. (2006), New Introduction to Multiple Time Series Analysis, Springer, New York.