Random Effects Model: Assumptions and GLS Estimation

The Random Effects Model is also sometimes called the Error Components Model or the Two-error structure approach. The Fixed Effects Model has some problems such as the use of dummy variables in the LSDV approach or the inability to include time-invariant independent variables. Hence, the Random Effects Model provides a different approach to account for cross-sectional and time-specific effects in panel data. The random effects model includes the cross-sectional and time-specific effects as random error components in the model equation.

The difference between the Fixed Effects Model and the Random Effects arises from one crucial assumption. The Random Effects model assumes that the cross-sectional and time-specific effects are independent of the explanatory variables. Hence, there is no correlation between the random error components and the independent variables. On the other hand, the cross-sectional and time-specific effects can be correlated with the independent variables in the Fixed Effects ‘Within’ Model.

Fixed and Random Effects Models

Econometrics Tutorials

Specification of the Random Effects Model

Random Effects Model with Cross-sectional and Time-specific Effects

We can express the Random Effects model with both cross-sectional and time-specific effects as:

In the equation, the intercept “α” is the mean intercept of all the cross-sections and time periods. Each individual “i” has a different value added to the mean intercept “α” to give the cross-sectional effects denoted by “μ_i“. Similarly, time-specific effects are represented by “v_t” and each time period “t” has a different value that is added to the mean intercept “α“.

Both the cross-sectional and time-specific effects given by “μ_i” and “v_t” are random error components in the above equations. That is, these effects capture the deviations of the individuals (cross-sectional units) and time periods from the mean intercept value of “α“.

This equation, however, cannot be estimated straightforwardly. It is just a simplified expression to illustrate the model. Furthermore, the Feasible Generalized Least Squares (FGLS) or Maximum Likelihood Approach estimate the Random Effects Model. Here, we will discuss the basics of the GLS estimation of the Random Effects Model.

the Random Effects Model: Estimation

First, let us consider a basic model with only cross-sectional effects:

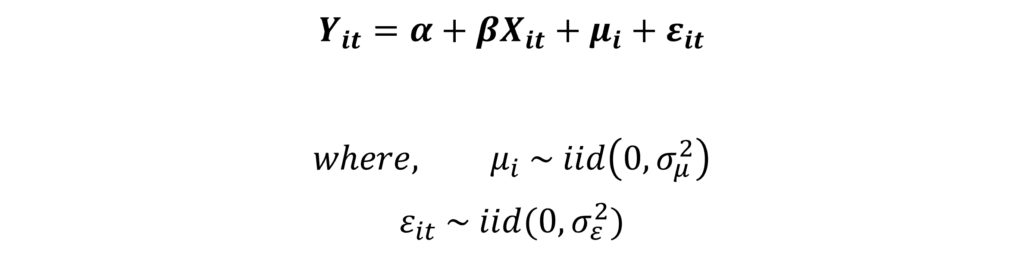
In this model, we have included only the cross-sectional or individual-specific effects using “μ_i“. The term “μ_i” is assumed to have a mean of 0 and variance “σ_μ²“, and is independently and identically distributed. The error “ε_it” is the usual residual or idiosyncratic error term that is independently and identically distributed with mean 0 and variance “σ_ε²“. The variances “σ_μ²” and “σ_ε²” of both the errors are crucial for the estimation of the Random Effects Model. Moreover, the model uses these variances to apply the GLS transformation.

GLS Transformation in the Random Effects Model

In Generalized Least Squares (GLS), we transform the variables in the model using some weights. For example, the Weighted Least Squares (WLS) Model is a special case of GLS where we transform using weights based on the nature of heteroscedasticity.

The weights in the Random Effects Model define the GLS transformation of variables:

In the Random Effects Model, we transform any variable “x_it” using “θ” as shown above. In turn, this “θ” is a function of the variances of the idiosyncratic error and the random error component. However, these weights must be estimated, they are not known to us beforehand. That is, we must estimate the “σ_μ²” and “σ_ε²” first, only then we can estimate the “θ” and transform the variables.

These variances (“σ_μ²” and “σ_ε²“) and “θ” are estimated using the Fixed Effects ‘Within’ Model and the ‘Between’ Effects Model. Hence, the estimation of the Random Effects Model is a combination of the ‘Within’ and ‘Between’ Effects models. Calculating the variances and the model can become complicated, so we will not discuss those here.

Considering everything, the estimation of the Random Effects Model using GLS is equivalent to estimating the following equation:

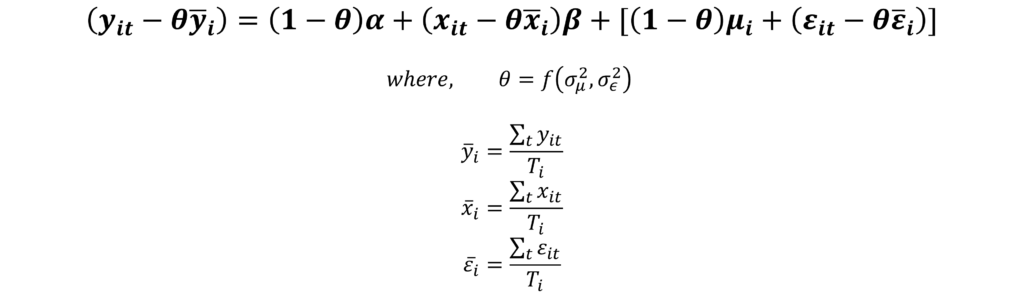
Software programs help us easily estimate this equation and its coefficients. They automatically take care of estimating the variances “σ_μ²” and “σ_ε²“, and “θ” first and then estimate the Random Effects Model. The reported results often contain the values of “θ“, “σ_μ²” and “σ_ε²” along with the coefficients.

Fixed Effects vs Random Effects Model

Critical Assumption: Fixed and Random Effects

The Random Effects (cross-sectional and time-specific) assume independence or no correlation to the independent variables in the model. If this assumption is violated and the effects are correlated to the independent variables, the Random Effects estimates are biased and inconsistent.

Therefore, we should avoid using the Random Effects model if the cross-sectional or time effects are correlated with any of the independent variables. In such cases, we can use the Fixed Effects model where these effects can be correlated to the independent variables.

Including the Time-invariant variables

As discussed in the Fixed Effects Model, we cannot include time-invariant independent variables in the Fixed Effects model because the fixed effects capture all the heterogeneity of the units. However, this is not the case in the Random Effects Model.

We can include time-invariant variables in the Random Effects model. This also gives it a huge advantage over the Fixed Effects model. The assumption stated above makes the random error components uncorrelated with the independent variables. Therefore, they do not interfere with the estimation of the coefficients of the time-invariant variables as they do in the Fixed Effects Model.

Choosing between Fixed and Random Effects

Finally, we need to know whether we should estimate the Fixed Effects or the Random Effects Model. We must decide which model is more appropriate based on the dataset and research objectives. This decision mostly comes down to 2 considerations.

First, we must decide the importance of time-invariant variables in our research. If we need to include certain time-invariant variables in our study, researchers may prefer the Random Effects model. This is because the Fixed Effects Model cannot accommodate time-invariant variables. Therefore, we may have to use the Random Effects Model or Correlated Random Effects model.

Secondly, we need to verify if we satisfy the critical assumption of the Random Effects model. If the cross-sectional or time effects are correlated with the independent variables, then we cannot use the Random Effects Model. We have to use the Fixed Effects mode in such a case. Here, we can use the Hausman Test to choose between the Fixed and Random Effects Models.

Further, we can also check whether the Random Effects are significant in the model or not. The Lagrange Multiplier Test for Random Effects can be used for this purpose.

Econometrics Tutorials