A time series is said to be stationary if its characteristics do not change with time. Moreover, a stationary time series can be identified as strictly stationary or weak stationary.
Strict vs Weak Stationarity
Strictly stationary time series: if the joint distribution of any bunch of time periods (xt, xt+1,…,xt+h) does not change with a shift in time (xt+i, xt+i+1,…,xt+i+h, where i = shift in time), the series is said to be strictly stationary. It is also sometimes referred to as strong stationarity. This can be very restrictive in nature, hence, many applications rely on weak stationarity.
Weak stationarity: weak stationarity requires a time series to have a constant mean, variance and autocovariance over time. Autocovariance gives the covariance of the time series with itself at a pair of time points or lags. For a stationary time series, this covariance remains the same as long as the lag or difference in chosen time periods remains the same. Mean, variance and autocovariance remain the same irrespective of the point of time we choose to measure them. That is, these characteristics are time-invariant in case of weak stationarity.
Econometrics Tutorials with Certificates
Non-Stationary time series
As the name suggests, a time series that is not stationary is called a non-stationary time series. The joint distribution, mean, variance or autocovariance of such a time series changes with time. Because the characteristics of the time series change with time, it becomes difficult to generalise the effects of variables to different time periods. Furthermore, a time series may be non-stationary due to a unit root, deterministic trend or seasonality. Hence, such a time series is generally not used for econometric analysis and forecasting.
In time series analysis, we often encounter non-stationary time series and it becomes essential to test for stationarity. If a time series is non-stationary, then, it must be transformed to make it stationary before proceeding further with analysis.
difference stationary and trend stationary time series
Difference stationary time series
A time series which becomes stationary after taking its first difference is called a difference stationary process. Random walk without drift is also an example of a difference stationary process.

Therefore, taking the first difference makes the model stationary as its mean and variance will be constant. Such a process is known as a Difference Stationary Process because taking the first difference makes it stationary. In some cases, a series must be differenced more than once to make it stationary.
Trend stationary time series
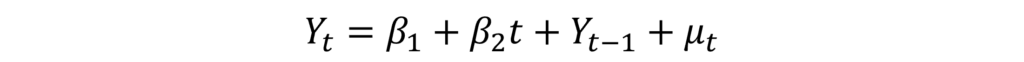
In the Random walk model with drift and deterministic trend, we have β1 as the drift parameter. This drift parameter (β1) grows over time at a constant rate shown by β2, which determines the trend of the time series Y. Hence, it is known as a Deterministic Trend because the values of the time series will oscillate around this trend.
If we take the first difference form, this time series will not become stationary.
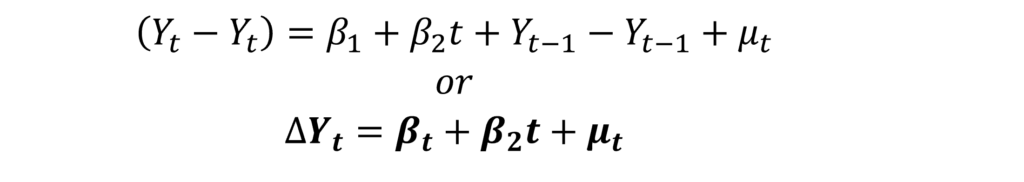
Here, the time series will have constant variance, but, it’s mean will not be constant. It will go on increasing over time due to the deterministic trend (βt+β2t). Hence, this time series will not be stationary in its first difference form.
As a result, a method known as detrending has to be used to eliminate non-stationarity from such a time series. Hence, it is known as a Trend Stationary Process.
making a time series stationary
| Reason for Non-stationarity | Type of process | How to make it Stationary |
| Unit root | Difference stationary | Take first difference |
| More than one unit roots | Difference stationary | Take higher-order differences |
| Deterministic trend | Trend stationary | Detrending |
| Seasonality | Seasonal cycles | Deseasonalize |
Apart from these methods to deal with non-stationarity, there are certain econometric techniques such as ARIMA, SARIMA, VAR, VECM models etc. that allow us to model trends and seasonality.
Related Posts
Econometrics Tutorials with Certificates
This website contains affiliate links. When you make a purchase through these links, we may earn a commission at no additional cost to you.


