The Random Walk Model is an example of a non-stationary time series. This model is often used to discuss as well as illustrate the concepts of stationarity, unit root process and order of integration.
Time series variables like stock prices, and exchange rates tend to follow a random walk process, which is non-stationary. Here, we will present three different types of random walk models – random walk without drift, random walk with drift and random walk with drift and deterministic trend. These models will, therefore, help you understand the concept of stationarity.
Econometrics Tutorials with Certificates
Random walk without drift
Firstly, a Random Walk Model without drift can be expressed as:
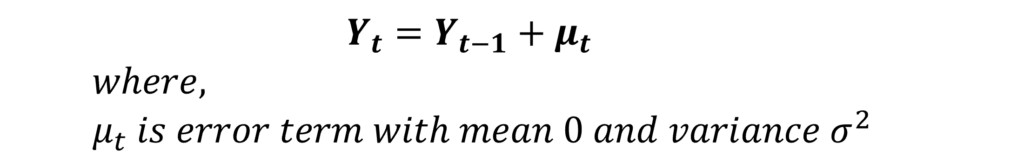
Here, the term μt is the white noise error term. Therefore, the value of variable Y is equal to its previous period value plus some random error or random shock.
Mean and Variance of Random Walk without Drift
If the time series started at time period 0, then:
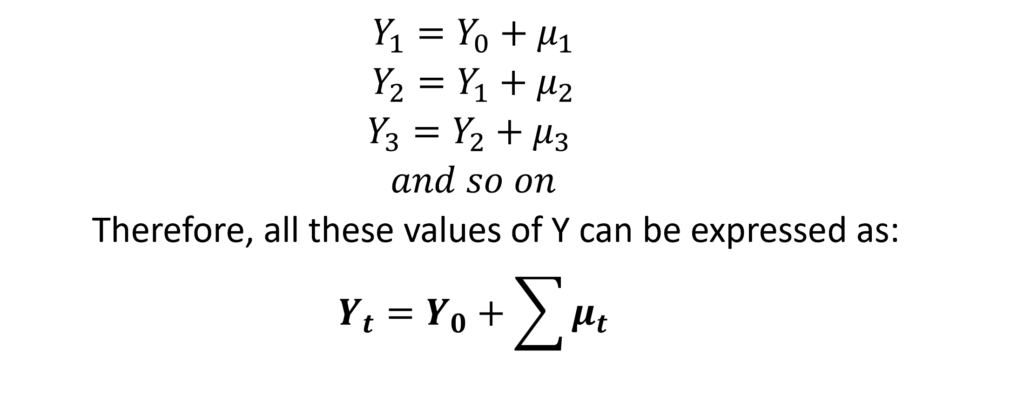
Hence, this means that every value of Y is simply a random shock added to the initial value of Y. With every time period, a new random shock is further added to update the value of Y. Moreover, the mean of Y will be its initial value Y0 because the error terms have zero expected value.
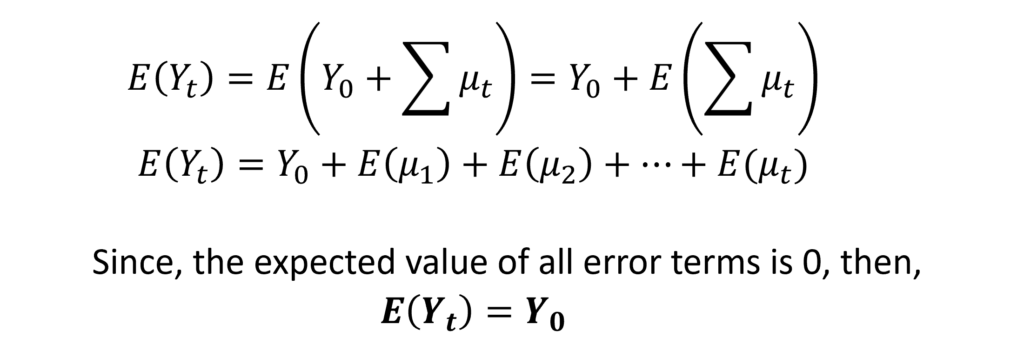
The variance of this Random Walk Model, however, increases with time.

With time, the variance will go on increasing. Therefore, Random Walk Model without drift is non-stationary time series. The Random Walk Model is said to have an infinite memory because the random shocks keep adding to the initial value over time. This is also why its variance goes on increasing. The effect of every random shock stays forever. For instance, if the error or random shock is 10 in a given period, then the value of time series Y will be higher by 10 units from the next time period onwards.
Random walk with drift
The Random Walk model with drift includes a drift parameter as follows:
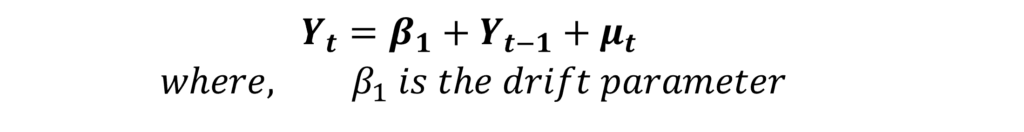
Therefore, the constant term is the drift parameter in this model. It is called drift because the time series Y will drift upwards or downwards depending on the sign of the constant. If it has a negative sign, the time series will drift downwards with time and it will drift upwards if the drift parameter has a positive sign.
The mean and variance of this model can be expressed in a similar way as Random Walk without drift:
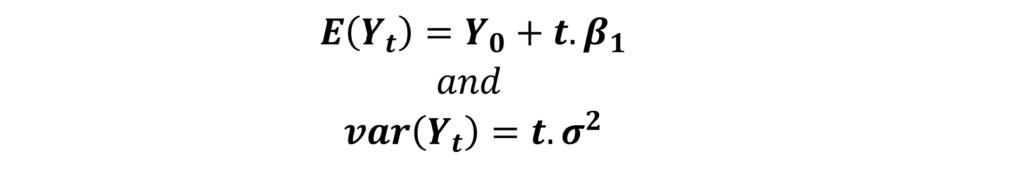
Hence, both the mean and variance will increase over time. Random Walk Model with drift is also a non-stationary time series.
Unit root
Let us further consider the following model:
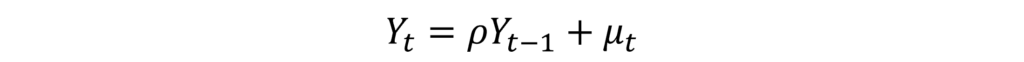
This model is an AR(1) model with ρ as the coefficient associated with Yt-1. If this coefficient ρ=1, then the model will reduce to a Random Walk Model without drift:
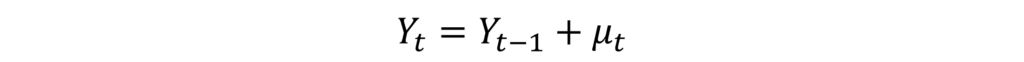
We already established that the Random Walk without drift is a non-stationary process. In such a case, we say that we have a unit root problem. The name “unit root” refers to the fact that our coefficient has a value of 1 (ρ=1) leading to the problem of non-stationary time series. Hence, the terms non-stationary and unit root are often used to refer to the same problem.
Solution to this non-stationarity
Random walk without drift and random walk with drift are difference stationary processes. This means that we can make these models stationary by taking their first difference. In the presence of a unit root as described above, taking the first difference eliminates the problem of non-stationarity.
In some cases, time series can have more than one unit root. Moreover, a unit root is sometimes observed even after taking the first difference and higher-order differences can help make the series stationary. For instance, if a time series has two unit roots, taking a second difference can remove non-stationarity.
Random walk with drift and Deterministic trend
Finally, a Random walk with drift and deterministic trend contains a time variable in the equation:
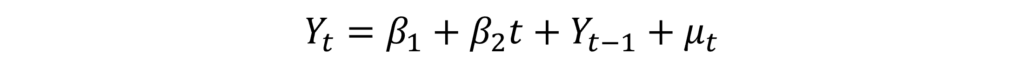
Similar to the previous model, β1 is still the drift parameter in this equation. However, we have an additional ‘time’ (t) variable in this equation which represents the deterministic trend. β2 is the coefficient associated with time. This means that the drift parameter will change at a constant rate with every time period. Moreover, this rate is determined by the trend coefficient (β2). Hence, the time series will revolve around this trend.
Because of this trend, the characteristics such as the mean and variance of the time series will not be constant over time. That is, the random walk with a deterministic trend will be a non-stationary time series.
However, taking differences will not make the series stationary. This is because of the deterministic trend component:
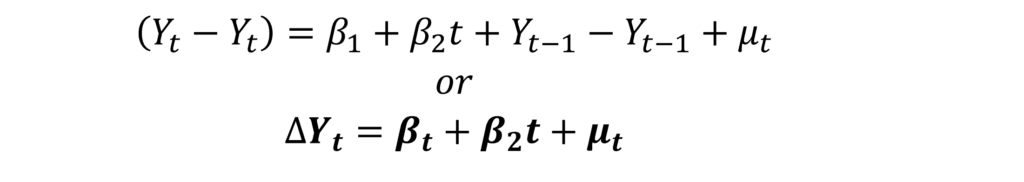
After taking the first difference, the variance of the time series will become constant. But, its mean will keep changing due to the trend component. Therefore, it will still not be a stationary time series. Hence, to make this type of series stationary, a method known as detrending is used to remove the trend component.
Econometrics Tutorials with Certificates
This website contains affiliate links. When you make a purchase through these links, we may earn a commission at no additional cost to you.



