The Shapiro Wilk test is a statistical test used to determine whether a sample or data comes from a normal distribution. Samuel Shapiro and Martin Wilk developed this test in 1965. They introduced this test in an article entitled “An Analysis of Variance Test for Normality (Complete Samples)“. The Shapiro-Wilk test is commonly used in various fields such as economics, finance, biology, and engineering to test the normality assumption of data.
Samuel Shapiro and Martin Wilk were both American statisticians. Samuel Shapiro was born in 1911 and earned his PhD in statistics from Columbia University in 1940. He further went on to work at the National Bureau of Standards, where he was involved in developing statistical methods for the analysis of data from experiments in physics and engineering. He was also a professor of statistics at the University of Illinois. Martin Wilk was born in 1922 and earned his PhD in statistics from Princeton University in 1951. He further went on to work at the University of California, Los Angeles (UCLA), where he made significant contributions to the development of statistical methods.
Econometrics Tutorials with Certificates
W Statistic: Shapiro Wilk test formula
The Shapiro Wilk test works by calculating the W statistic. The W statistic measures the discrepancy between the observed data and the expected values under a normal distribution. Moreover, the test statistic ranges between 0 and 1, with values closer to 1 indicating a closer fit to a normal distribution. We can calculate the W statistic using the following formula:
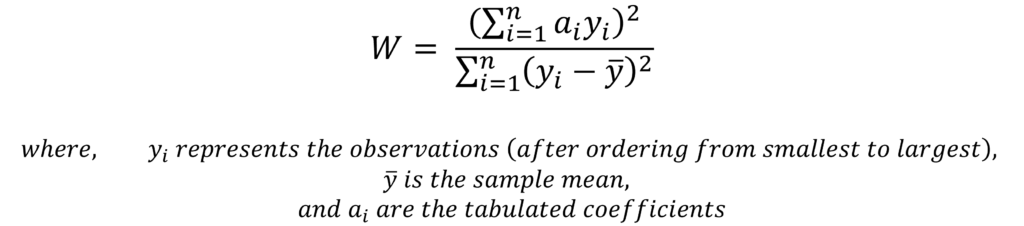
The W statistic is used to test the following hypotheses:
H0: the sample data is normally distributed
HA: the sample data is not normally distributed
The tabulated coefficients “ai” and the critical values for the Shapiro Wilk test can be obtained from the tables. These values are based on the number of observations in the sample. Furthermore, we do not need to do any steps manually and the statistical software packages make the entire application easy.
We reject the null hypothesis of normality if the W statistic is less than the critical value from the table. Hence, the sample data is not normally distributed in such a case. However, if the W statistic is greater than the critical value, we cannot reject the null hypothesis. As a result, we can conclude that the sample data is normally distributed.
Application of the Shapiro Wilk test
Statistical software packages make the application and interpretation of the Shapiro Wilk test straightforward. Moreover, we do not need to look up the values of tabulated coefficients “ai” or the critical values manually. The software takes care of all the steps automatically.
Although we usually do not need to estimate the W statistic manually, we should still understand how the test works. Therefore, we will illustrate the application of the test along with all the steps involved using a small sample:
Step 1: Order the observations from the smallest to the largest
Suppose, we have the following hypothetical sample of 8 observations:
| Observations | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Sample | -3 | 4 | 8 | 1 | 2 | 5 | -4 | 3 |
| Ordered from smallest to largest | -4 | -3 | 1 | 2 | 3 | 4 | 5 | 8 |
The first row shows the number of observations of the sample. To apply the Shapiro Wilk test, we must order these observations in ascending order. The ordered observations from the smallest to the largest are shown in the second row.
Step 2: estimate the sum of (𝑦𝑖−𝑦 ̅ )2
The value of 𝑦 ̅ shows the mean of the sample. In this sample, it is equal to 2.
| Observations | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Sample | -3 | 4 | 8 | 1 | 2 | 5 | -4 | 3 |
| (𝑦𝑖−𝑦 ̅ )2, where 𝑦 ̅ = 2 | 25 | 4 | 36 | 1 | 0 | 9 | 36 | 1 |
Therefore, the sum = 25 + 4 + 36 + 1 + 0 + 9 + 36 + 1 = 112
Step 3: Use the tabulated coefficients ai
Further, we have to calculate the following:
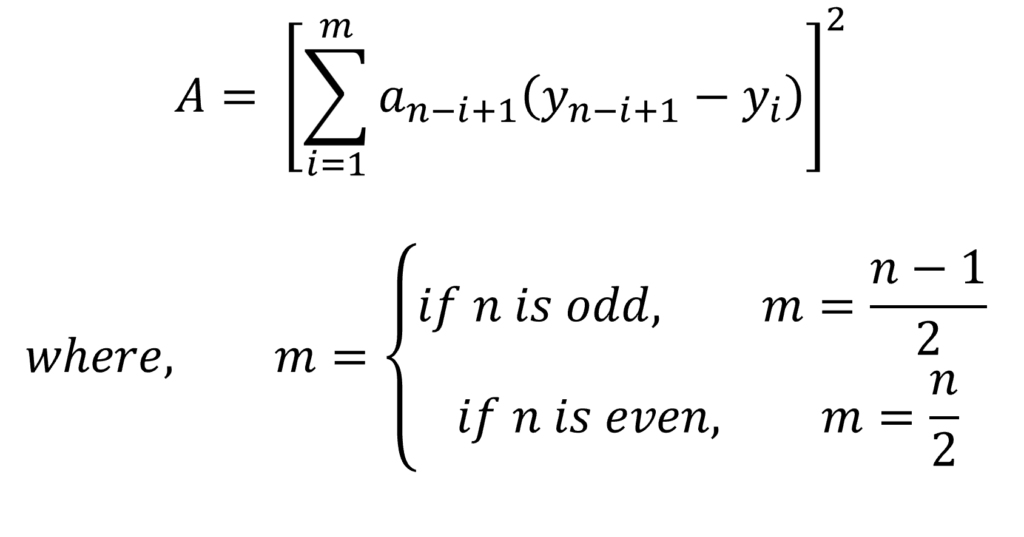
This formula uses the coefficients “ai” which can be obtained from the tables given by Shapiro and Wilk, or further contributed by others. These coefficients have been tabulated and extended by several statisticians over the years. In our example, we have 8 observations. This means that n = 8 in our example, hence, m = 4.

Step 4: estimate the W statistic
We can estimate the Shapiro Wilk test statistic (W) using the values obtained above:
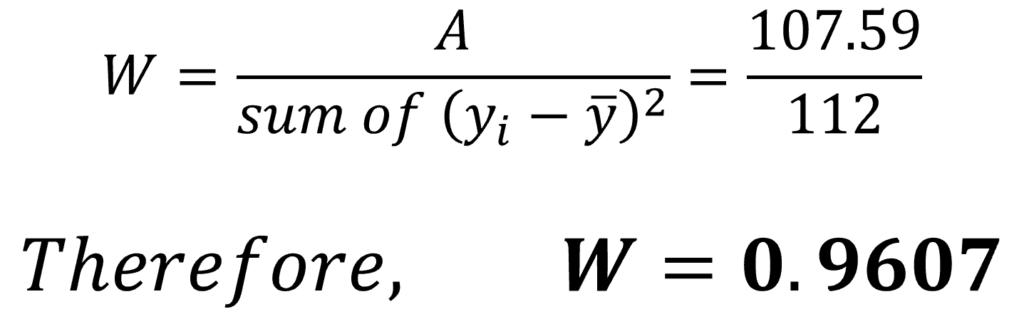
Hence, we have calculated the W statistic for our sample. W = 0.9607 is very close to 1, indicating that our data sample might be normally distributed. However, we should still compare W with the critical values of the test.
Step 5: compare W with the critical values
Earlier, we mentioned the hypothesis tested under Shapiro Wilk test. We can state that hypothesis as follows:
H0: the sample data is normally distributed
HA: the sample data is not normally distributed
We can test the above hypothesis by comparing the W statistic with the critical values. The critical values of the Shapiro Wilk test are available in the tables here.
We can see from the table that the critical value is 0.932 at the 0.50 level. if we consider the 0.05 level, then the critical value is 0.818. Generally, a critical value at 0.05 level is used. Therefore, we can see that the W statistic (0.9607) is greater than this critical value (0.818). Hence, we cannot reject the null hypothesis and conclude that the data is normally distributed.
Advantages and limitations of the Shapiro Wilk test
Advantages
- Good power: The Shapiro-Wilk test is known to have good power (i.e., the ability to detect non-normality) compared to other tests of normality, especially for small to moderate sample sizes.
- Applicability to small sample sizes: The Shapiro-Wilk test is also effective for small sample sizes, making it suitable for many research settings.
- Theoretical basis: The Shapiro-Wilk test is based on a well-established theoretical framework that provides a solid foundation for interpreting the results and making statistical inferences.
- Easy to use: The Shapiro-Wilk test can be easily implemented in most statistical software packages, making it a convenient choice for researchers and practitioners.
Limitations
- Sensitivity in large samples: The Shapiro-Wilk test is highly sensitive to even small deviations from normality in large samples. This means that as the sample size increases, the test becomes more likely to reject the null hypothesis of normality, even if the deviations from normality are very small. While this sensitivity can be useful for detecting even subtle departures from normality, it can also be a limitation of the test in certain situations. For example, if the sample size is very large, even small departures from normality may be statistically significant, even if they are not practically meaningful. In such cases, it must be supplemented by other tests such as the Kolmogorov-Smirnov test, Anderson-Darling test etc.
- Interpretation of results: While the Shapiro-Wilk test indicates whether or not the data appears to be normally distributed, it does not provide information about the extent or nature of deviations from normality, nor does it identify the causes of any observed deviations.
Econometrics Tutorials with Certificates
This website contains affiliate links. When you make a purchase through these links, we may earn a commission at no additional cost to you.


