Cointegration refers to the situation where the variables have a long-run or equilibrium relationship. Such variables move together over time and can be said to have a similar wavelength or share a common trend. Equilibrium and long-run relationships hold special significance in Economic theory. Cointegration is a desirable property because of this reason.
In the short run, the variables might be in disequilibrium and can diverge from their equilibrium position. However, they have a tendency to converge towards their long-run equilibrium if they are cointegrated.
Defining cointegration
Let us consider a two-variable model. Suppose the two variables Yt and Xt are non-stationary and integrated processes as follows:
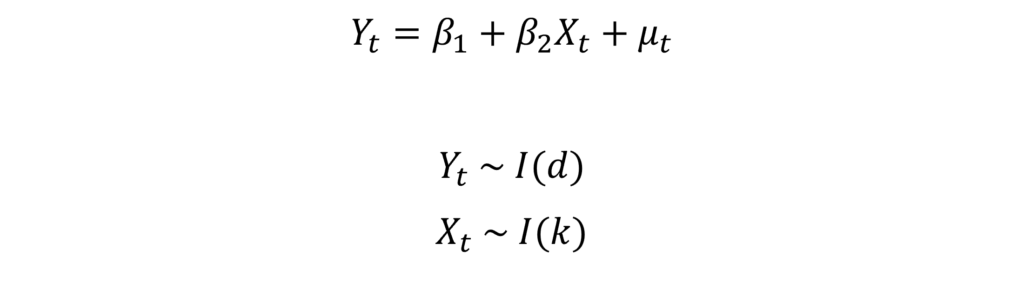
We say that these variables are cointegrated if “d = k” and a linear combination of these variables is stationary or has a lower order of integration than “d=k”. Hence, this implies that both variables have the same order of integration (d = k). Furthermore, their linear regression yields a stationary error term if they were I(1) or d = k = 1:
μt ~ I(0)
The variables Yt and Xt are cointegrated in this case. That is, they have a long-run equilibrium relationship. Even though both time series are non-stationary when considered individually, but, their linear combination is stationary. Hence, the t-test and other usual tests are applicable to such a model with cointegrating variables. Otherwise, these tests would have been unreliable due to the non-stationarity of individual time series variables.
The coefficient estimates of β1 and β2 in the model are long-run estimates. β1 is the long-run intercept and β2 shows the long-run relationship between Yt and Xt. These coefficients are sometimes referred to as cointegrating parameters. Suppose, the variables are integrated of order 2 (d = k = 2) and their combination gives an I(1) error term. Then again, we can say that the variables are cointegrated.
Further considerations: Tests and models for cointegration
Cointegration Tests: Engle-Granger, Johansen and ARDL approach
It is essential to test for cointegration among time series variables. If the variables are cointegrated, the entire approach to model specification and estimation is different.
For a simple two-variable model like the one above, the Engle-Granger test of cointegration is applicable. The major disadvantage of this test is that it cannot be applied if we have more than two cointegrated relationships in the model. In such cases, we have to employ Johansen’s Test of Cointegration. It allows us to detect multiple cointegrating relationships among variables. Suppose we have 4 time series variables. It is possible that some of those variables have a long-run relationship with each other and others do not. The Johansen Cointegration Test can detect such multiple cointegrating variables.
Even this test is not without its faults. For Johansen’s approach to work, all variables must have the same order of integration. If any variable has a different order of integration, we cannot use the Johansen Test. For instance, we might have 3 variables that are I(1) and can be cointegrated with each other but one more variable that is I(2) in the model. Then, we cannot apply this test to all 4 variables because one of them is I(2).
However, we can still test for cointegration and obtain the long-run estimates using the ARDL (Autoregressive Distributed Lag) approach. This is often used when some of the variables have a different order of integration. The disadvantage of this approach is that it is not applicable to multiple cointegrating relationships.
Models for Cointegration: Error Correction, VECM and ARDL
The Error Correction Mechanism can be employed for modelling the long-run as well as the short-run relationships. A simple error correction approach with the help of ARDL can be used in the case of one cointegrating relationship. If we have more than one long-run relationship, we can estimate a VECM model.
The Vector Error Correction Mechanism or VECM allows us to model multiple cointegrating relationships. It gives us short-run as well as long-run estimates of the variables. This model is based on Johansen’s Cointegration Test and extends it further. We can detect multiple cointegration or long-run relationships using Johansen’s Test and then apply VECM to estimate the parameters. Similar to the test, the variables must have the same order of integration for this approach.
If there are certain variables with different orders of integration, we have to resort to the ARDL approach. Hence, ARDL approach lets us estimate the long-run coefficients for variables that have different orders of integration.
Econometrics Tutorials with Certificates
This website contains affiliate links. When you make a purchase through these links, we may earn a commission at no additional cost to you.




