Autocorrelation occurs when the error terms in the model exhibit correlation or dependency on each other. That is, errors in previous periods influence the errors in the current period. Economists commonly face this issue due to the nature of time-series data, where the values of variables and error terms from prior periods impact the values in the current period.
One of the assumptions of OLS states that there should be no autocorrelation in the model. It is also referred to as serial independence. Serial independence means that the error term in any given period is independent of error terms of other periods. That is, error terms do not affect each other.
Autocorrelation may also exist in cross-sectional data, but it is mostly observed in time series analysis. This is because the error term associated with one observation generally does not affect other observations in cross-sectional data. It is important to note these differences in the presence of autocorrelation in different types of data analysis. Consider the example of consumption, change in consumption of one household due to a random factor (like winning a lottery) will not affect the consumption of other households.
Autocorrelation vs Serial Correlation
The terms autocorrelation and serial correlation are usually used synonymously. But, there is a theoretical distinction between the two. Autocorrelation occurs when a time series variable’s current value depends on its own past values. On the other hand, serial correlation is a situation where the current value of a time series variable is dependent on the lagged values of another time series.
Econometrics Tutorials with Certificates
Causes Of Autocorrelation
- Omission of important independent variable: If the model does not include an important independent variable, then the error term captures its effects. This leads to dependencies between errors if the excluded variable is autocorrelated. Time series variables often exhibit autocorrelation due to their inherent nature. For example, income in the current period generally depends on the previous period’s income. If we exclude the income variable from the consumption function, autocorrelation may affect the model. This is because the income variable we leave out is likely autocorrelated and is captured by the error terms. In other words, excluding the income variable can lead to autocorrelation impacting the model’s accuracy.
- Nature of problem: in some cases, error terms are autocorrelated due to the nature of economic phenomenon. Let us consider an example of agricultural production and droughts. Drought, here, is a random factor that might end up causing autocorrelation. This is because the drought will affect production not only in the current period but also in the next periods. Hence, autocorrelation may exist because certain random factors have their effects over a longer period or across more than one time periods.
- Mis-specification of functional form: a wrong functional form of the model may also cause autocorrelation. For example, if the true relationship between variables is cyclical, but, the model uses a linear functional form. In such a case, the error terms might become correlated as the cyclical effects are not addressed by the explanatory variables.
- Non-stationarity: a time series is stationary if its features (such as mean and variance) are constant over a given period of time. If the time series variables in a model are non-stationary, then, the error term may also be non-stationary. As a result, varying characteristics (mean, variance, covariance etc.) over time might autocorrelate with the error term.
Consequences Of Autocorrelation
- Underestimation of Residual Variance: the variance of the error term is underestimated if the errors are autocorrelated. If the autocorrelation is positive, then this problem can become even more serious.
- Variance of estimates: in the presence of autocorrelation, the estimates of Ordinary Least Squares or OLS are still unbiased. However, the variance of the estimates will likely be larger than in the case of other methods. In the presence of autocorrelation, parameters exhibit a larger true variance, while the OLS formula underestimates the estimated variance. The variance of coefficients is smaller than their true variance. That is, we have an underestimation of the parameter or coefficient variance.
- Tests of significance: usual tests of significance like standard errors, t-test and F-test will give misleading results and are no longer reliable because the variance of coefficients is underestimated. One cannot use these tests to establish the statistical significance of coefficients. The estimated standard errors will be smaller because of underestimated variance, thereby, affecting t-values as well.
- Predictions: In autocorrelation, the OLS model’s predictions will be inefficient. This means that the predictions will have a larger variance as compared to predictions from other models like GLS.
Detection
Durbin-Watson d Statistic
This test is applicable to the first-order autoregressive scheme where the error terms are dependent on the previous one-period error only. The first-order autoregressive scheme means that the error is dependent on the previous one-period error.
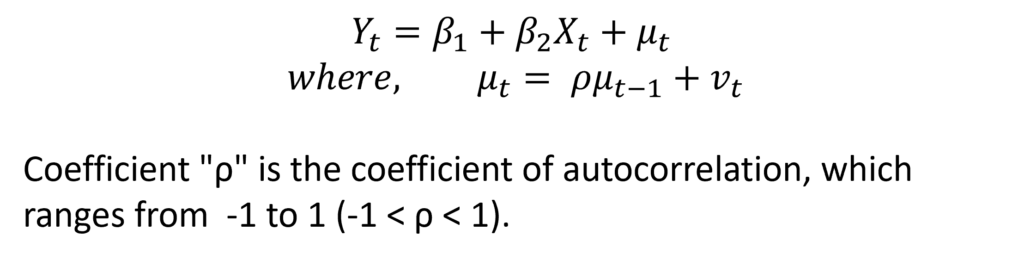
For such a model, the Durbin-Watson d statistic is:
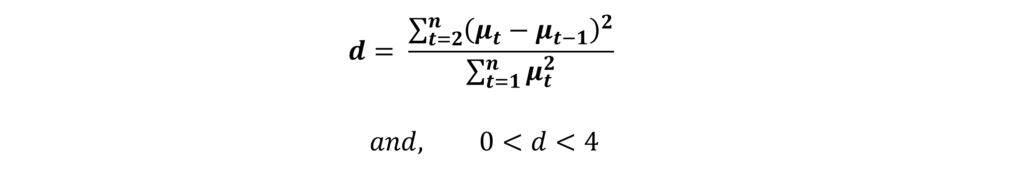
Therefore, the value of this Durbin-Watson d statistic lies between 0 and 4. The value of d = 2 means that there is no autocorrelation and ρ = 0. On one extreme, the value of d will be 0 when ρ = +1, which implies a perfect positive autocorrelation. On the other extreme, when ρ = -1, d will be equal to 4, which indicates a perfect negative autocorrelation.
However, this test has some serious limitations:
- It applies to first-order autocorrelation scheme only.
- The error terms must follow a normal distribution.
- In the model, we must not include the lagged values of the dependent variable.
Breusch-Godfrey LM Test
This test tries to overcome the limitations of the Durbin-Watson d statistic. It is applicable to higher-order autoregressive schemes, moving average models and models with lagged values of the dependent variable.
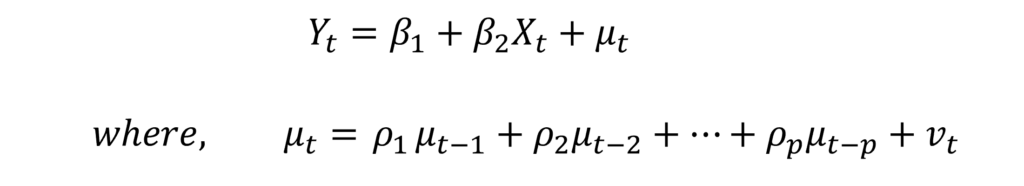
This model is autoregressive of order “p” or pth-order autoregressive scheme because it includes “p” lagged values of the error term.
The LM test follows the following procedure:
Step 1: estimate the simple OLS model and obtain residuals μ ̂t
Step 2: regress μ ̂t on all the independent variables (Xt in this example) and lagged values of error term determined by the order of autoregressive scheme (μ(t-1), μ(t-2),…, μ(t-p) in this example).
Step 3: obtain R2 of this regression.
Step 4: in a large sample size,
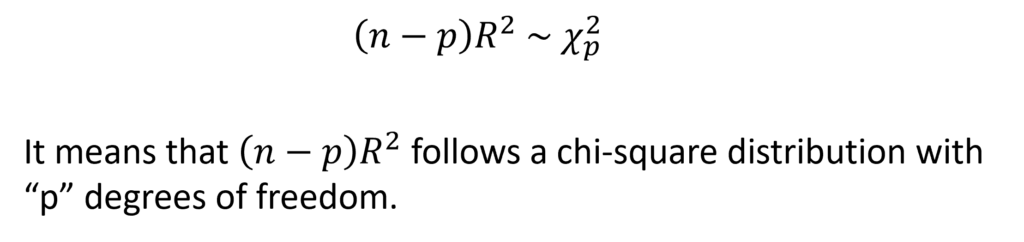
If this value exceeds the critical chi-square value at the chosen level of significance, at least one of the lagged values of the error term is significant. Therefore, we reject the null hypothesis of no autocorrelation and we know that autocorrelation exists.
Autocorrelation Function, ACF and PACF plots
We can also use the autocorrelation function on the residuals to detect the presence of autocorrelation. Additionally, one can use autocorrelation function plots (ACF plots) and partial autocorrelation function plots (PACF plots) to understand the autoregressive and moving average behaviour of the time series. Usually, these methods help in assessing the stationarity of time series variables. You can learn more about these methods from Autocorrelation Function and Interpreting ACF and PACF Plots.
Solutions
The omission of important explanatory variables or wrong functional forms can cause autocorrelation. In such cases, including the omitted variables or trying different functional forms can eliminate the problem. However, dealing with pure autocorrelation is not straightforward because it can be inherent in time series variables. Some of the methods that can be employed are as follows:
Newey-West Standard Errors
Newey-West standard errors are also known as Heteroscedasticity and Autocorrelation consistent (HAC) standard errors. These standard errors correct for both heteroscedasticity and autocorrelation, extending White’s Heteroscedasticity consistent standard errors to account for these issues.
Because Newey-West standard errors correct for autocorrelation as well as heteroscedasticity, it allows researchers to use the usual t-test and p-values to determine the significance of coefficients. Newey-West standard errors are larger than OLS standard errors because of underestimation by OLS standard errors.
Note: Newey-West standard errors should be applied to large samples only. They should not be used in small samples.
Feasible Generalized Least Squares
The application of Generalised Least Squares in the presence of autocorrelation is also referred to as Feasible Generalised Least Squares (FGLS). The idea of this method is similar to Weighted Least Squares (WLS) in the presence of Heteroscedasticity. The model assigns weights to the variables in a way that eliminates the effect of autocorrelation.
The weights are determined by the autocorrelation coefficient (ρ) and are used to transform the model. Let us consider the simple two-variable model with a first-order autoregressive scheme, i.e. AR(1).
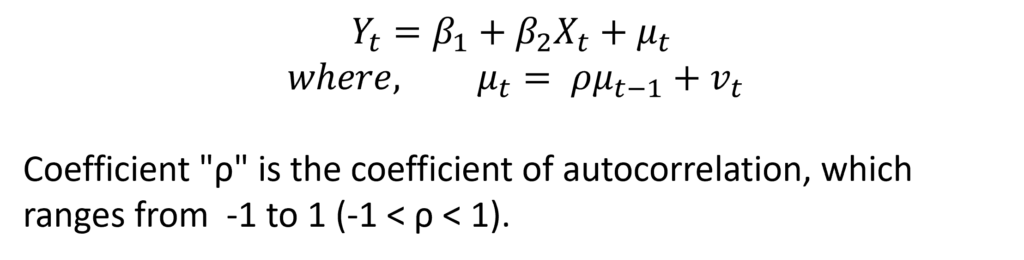
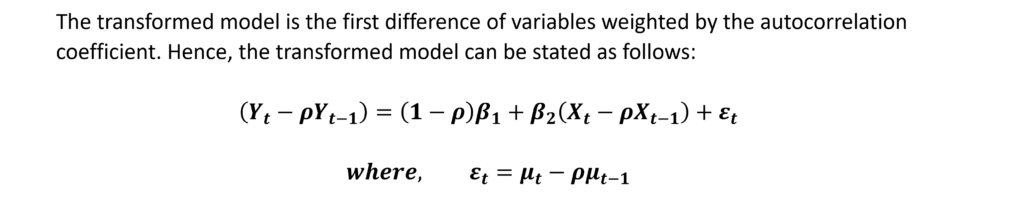
In practice, the “p” coefficient is unknown and must be estimated. Several methods can be used to accomplish that such as the Durbin-Watson d statistic or the Cochrane-Orcutt method. If the “p” coefficient is almost one, we can simply use the first differences.
Time Series Models
Time series models are one of the most essential techniques for economists involving the study of stationarity, cointegration and specialised models to deal with time series. These include ARMA, ARIMA and SARIMA models. Furthermore, multiple equation models for time series such as VAR and VECM can be employed by economists to study multiple relationships and cointegration.
Econometrics Tutorials with Certificates
This website contains affiliate links. When you make a purchase through these links, we may earn a commission at no additional cost to you.


