The Mann Whitney U Test is also sometimes referred to as the Wilcoxon Rank Sum Test. It is a nonparametric test used to compare two independent groups or samples. In this sense, the Mann Whitney U test or Wilcoxon Rank Sum test is a nonparametric alternative to the Independent t-test. It was developed by Henry Mann and Donald Whitney, and independently by F. Wilcoxon in the 1940s.
Nonparametric tests do not make any assumptions about the distribution of the samples. These tests are good alternatives when the assumptions of the parametric tests are not met. For instance, the independent t-test needs the data to be normally distributed. The Mann Whitney U test/Wilcoxon Rank Sum test is a good alternative for samples that are not normally distributed.
This website contains affiliate links. When you make a purchase through these links, we may earn a commission at no additional cost to you.
Statistics 1 Part 1: Introductory Statistics, Probability and Estimation
Statistics and R
MathTrackX: Statistics
Statistics Using Python
requirements for the mann whitney u test
The Mann Whitney U test or Wilcoxon Rank Sum test is applicable in situations where:
- The two groups or samples are independent.
- The data must be ordinal or continuous, hence, it cannot be nominal data.
- It does not need the samples to be of the same size. That is, the groups or samples can have different sizes or observations.
- The data does not need to be normally distributed. However, it does require the data to be independent and identically distributed or i.i.d. This implies that the data or samples are drawn from the populations with the same distribution (it does not have to be a normal distribution).
The test can be applied after considering the above requirements. It is important to note here that the usual parametric tests like the Independent t-test are more powerful if their assumptions are met. But, nonparametric tests like the Mann Whitney U test are much more flexible because they do not make many restrictive assumptions.
Implementation of the Mann Whitney U test
While the Independent t-test is based on calculating the means, the Mann Whitney U test or Wilcoxon Rank Sum test is median-based. The procedure for applying the test and calculating the U statistic is as follows:
Step 1: Formulate the hypothesis
The hypothesis of the test can be stated depending on the context of the problem. However, the hypothesis of the test can be stated in general terms:
H0: no significant difference between the medians of the two groups.
HA: there is a significant difference between the medians of the two groups.
A 5% level of significance is commonly used in the interpretation of the hypothesis.
Step 2: Rank the observations of the groups and calculate the sum of the ranks
All the observations from the two groups or samples are combined and ranked. Rank 1 is assigned to the smallest observation, Rank 2 to the second smallest one and so on. In this way, all the observations from the two samples are ranked and the sum of the ranks is calculated for each sample.
As a result, we will obtain two values for the sum of the ranks. If we have groups A and B, the sum of the ranks will be given by RA and RB. Here, RA is obtained by adding the ranks of the observations of Group A. Similarly, RB is calculated by adding all the ranks of Group B observations.
Step 3: Calculate the test statistic U
After calculating the sum of the ranks, we can estimate the values of UA and UB as follows:
Therefore, the test statistic U is chosen from UA and UB. If UA is smaller as compared to UB, the UA is used as the test statistic U and vice versa.
Step 4: Compare U with the critical value and estimate the P-value
The test statistic U is compared with the critical value from the significance tables. The statistical software packages also provide the P-values by default which makes the interpretation of the test easier.
If the P-value is greater than 0.05 (using a 5% significance level), we cannot reject the null hypothesis. As a result, we conclude that the medians of the two groups are not significantly different. In this case, the U statistic will be greater than the critical value from the table.
On the other hand, we reject the null hypothesis if the P-value is less than 0.05 and the U statistic is less than the critical value from the table. Then we can conclude that the medians of the two groups or samples are significantly different.
Example
Suppose an Agriculture Economist wants to compare the effects of synthetic and organic manure on agricultural productivity. The data consists of 14 observations with 2 groups of farmers who use Synthetic and Organic manure. Group A uses Synthetic manure whereas Group B uses Organic manure for their crops. The 14 observations represent the per-acre productivity of the 14 farmers from both groups.
| Per-Acre Productivity | |||||||
| Groups | |||||||
| Group A: Synthetic Manure | 25 | 34 | 23 | 67 | 54 | 40 | 36 |
| Group B: Organic Manure | 45 | 68 | 90 | 57 | 61 | 46 | 77 |
To analyze whether there is a significant difference between the productivity of farmers using Synthetic and Organic manure, the Economist can apply the Mann Whitney U test or Wilcoxon Rank Sum test.
Step 1: Formulate the hypothesis
The hypothesis of the test depends on the problem that the Economist wants to study. As a result, the statement of the hypothesis can differ depending on the type of analysis and focus of the study. As a simple example, we will formulate a straightforward hypothesis:
H0: no significant difference between the productivity of Synthetic and Organic Manure
HA: there is a significant difference between the productivity of Synthetic and Organic Manure
Important: the statement of Alternate hypothesis (HA) can be different for different cases. For instance, the Economist can formulate a hypothesis that the productivity of Organic Manure is significantly higher than Synthetic Manure. As a result, the interpretation of the test can change due to the hypothesis. Moreover, the choice of a One-tailed or Two-tailed test can depend on the type of hypothesis. Hence, the choice of the hypothesis must be carefully considered. A One-tailed test is used if the direction (higher/lower or greater/smaller etc.) is specified in the alternate hypothesis. The critical values of the Mann Whitney U test are different for One-tailed and Two-tailed tests.
In our example, we will use a Two-tailed test because we have not specified any direction in the alternate hypothesis.
Step 2: Rank the observations and calculate the sum of the ranks
| Observations | 23 | 25 | 34 | 36 | 40 | 45 | 46 | 54 | 57 | 61 | 67 | 68 | 77 | 90 |
| Rank | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Group | A | A | A | A | A | B | B | A | B | B | A | B | B | B |
All 14 observations have been ranked from the smallest to the largest based on productivity. The “Rank” row represents the rank of each observation. The “Group” row identifies the group of the observation (synthetic or organic) in the table. The sum of the ranks of each group can be calculated as follows:
The sum of the ranks of Group A (Synthetic) = RA = 1 + 2 + 3 + 4 + 5 + 8 + 11 = 34
Hence, RA = 34
The sum of the ranks of Group B (Organic) = RB = 6 + 7 + 9 + 10 + 12 + 13 + 14 = 71
Hence, RB = 71
Step 3: Calculate the test statistic U
The test statistic can be easily estimated using the formulas above:
This value of the U statistic can be compared to the critical value to obtain the results.
Step 4: Compare with critical value and make conclusions
The critical value of the statistic at a 5% level of significance for a Two-tailed test is 8. The number of observations in each group is used to find the critical value from the significance table. You can find the significance table here.
Our test statistic U is 6, which is less than 8. That is, our test statistic is less than the critical value at a 5% level of significance. This means that we can reject the null hypothesis. Therefore, the Economist can conclude that there is a significant difference between the productivity of farmers due to synthetic and organic manures.
Moreover, it is clear that the productivity levels are mostly higher for Organic Manure users. As a result, the Economist can also conclude that Organic manure leads to higher productivity levels as compared to synthetic manures.
The probability that Group A’s productivity will be greater than Group B’s productivity
We can also easily estimate the probability that the productivity level of a synthetic user will be higher than the productivity level of an Organic manure user.
Probability = U / (nA*nB) = 6 / (7*7) = 6 / 49 = 0.122
Hence, 0.122 is the probability by which synthetic manure will give higher productivity than organic manure. As expected, this probability is very low because we observed significantly higher productivity levels for organic manure.
Large samples: Normal approximation and z scores
The significance tables usually give critical values for small samples only. Usually, you will see tables of up to 20 observations per group which means that we need an alternative for large samples. This is where we can employ normal approximation and calculate z values in case of large samples. The z values can help us make conclusions by comparing the z value with its critical value and also calculating p-values. We can use z values for this purpose because U approaches a normal distribution with large samples.
The formula for normal approximation after Mann Whitney U test to obtain a z score is as follows:
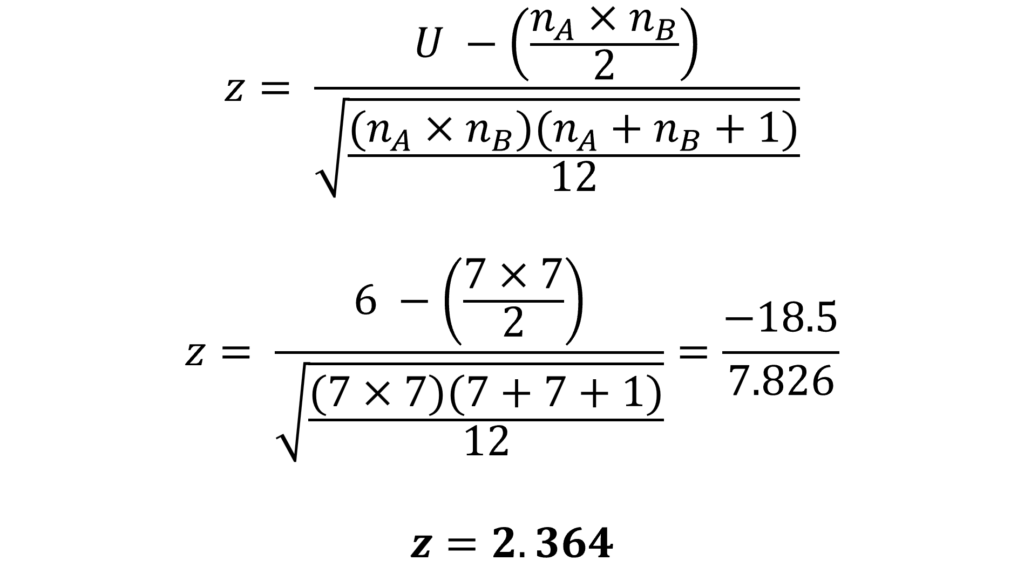
This z score can be used to test the same hypothesis by comparing it with the critical value or by computing the p-value. What’s more, most Statistical software packages provide the z-scores and p-values by default.
For our example, the normal approximation gives us a z-value of 2.364 and a p-value of 0.0181. We can reject the null hypothesis because the p-value is less than 0.05 (at a 5% level of significance). Hence, our results and interpretation stay the same with normal approximation as well.
advantages and limitations of the Mann Whitney u test/Wilcoxon rank sum test
Advantages
- Nonparametric nature: it does not make any prior assumptions about the distribution of the data. This makes the test more robust to the presence of outliers in the data or any deviations from the normal distribution. Its parametric alternative (independent t-test) is sensitive to such deviations and outliers.
- Small samples: the Mann Whitney U test or the Wilcoxon Rank Sum test can be applied to small samples as well and limited sample size is not a problem for researchers when applying this test.
- Different sample sizes: the test does not need the two groups or samples to have the same number of observations. It can be applied even if the group sizes are different.
Limitations
- Independent observations: one of the assumptions of the test is that the observations are independent of each other. This may not hold true in several practical cases because it is common to observe some dependence between observations. Therefore, the test cannot be applied in such a situation.
- Less powerful: as in the case of most nonparametric tests, it is less powerful than its parametric alternative. If the assumption of a normal distribution is met along with other assumptions, the Independent t-test is more powerful. In addition, the Mann Whitney U test will require a much larger sample to have the same level of power as the independent t-test.
