Blog

The Linear Probability Model is an application of Ordinary Least Squares to qualitative response or dependent variables. We often encounter dependent variables that are continuous, such as income or consumption, and estimate them using methods like OLS, time series and panel data models. However, dependent variables are not always continuous or quantitative. We often have to deal with dependent variables that are qualitative, where we have dummy variables or categorical variables instead of continuous variables.

For example, suppose we want to study the effects of independent variables like age, education and experience on the employment decision of a company. Then, we have a binary dependent variable which can be coded as 1 if the person is hired and 0 if a person is not hired by the company. Therefore, we have 2 categories in the dependent variable which take the value of either 1 or 0.

Similarly, we might have a dependent variable with multiple categories. For instance, suppose we want to study the voting choice among 4 different political parties. Then, we will have a categorical dependent variable with 4 values of 0, 1, 2 or 3. Each value will represent a vote for a different political party (0 for party A, 1 for party B, 2 for party C and 3 for independent).

We have used dummy or categorical variables as independent variables in several models to account for different effects, like intercept dummies in fixed effects models. Here, we will discuss the estimation of the Linear Probability Model or LPM with a dummy or binary categorical variable as the dependent variable. We will illustrate why OLS is not appropriate for such models. We will also discuss why we should use the Logit and Probit Models in such cases.

Linear Probability Model Specification

Let us consider a simple model of an individual owning or not owning a car.

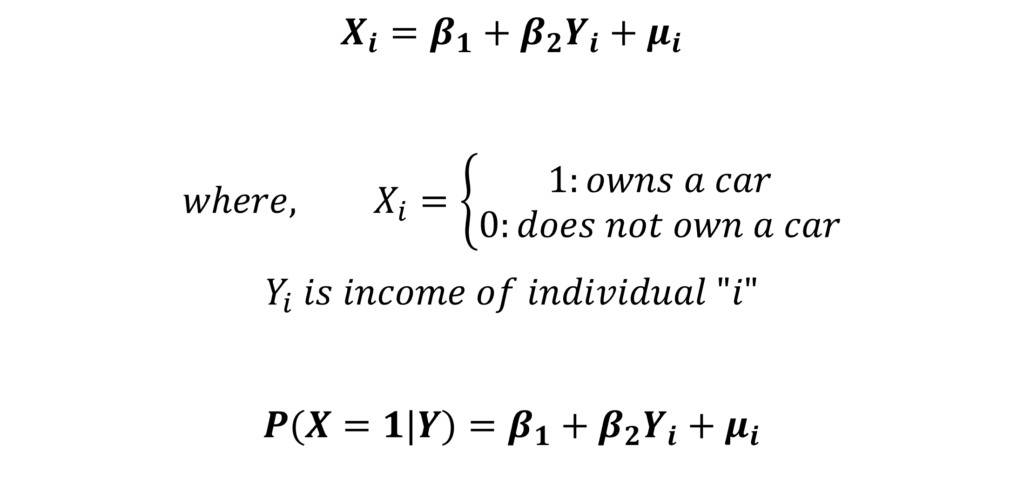
In the equation, the dependent variable X represents whether an individual owns a car or does not own a car. This variable is a function of the independent variable income, that is, the ownership of a car depends on the income of the individual. We have included only income as the independent variable for simplicity. In reality, ownership of a car depends on several other factors that should also be included in the model.

If an individual owns a car, then the dependent variable X is equal to 1. The dependent variable X is equal to 0 if an individual does not have a car. Therefore, X is a binary or qualitative variable. Estimating this model using Ordinary Least Squares is known as LPM or the Linear Probability Model.

The probability of success, probability of owning a car or probability that X equals 1 is a linear function of independent variables. We express this probability as “P(X = 1| Y)”, which means the probability of X equals 1 or the probability of owning a car equals 1 given the income Y. Hence, the predictions from this LPM give us the conditional probability of X equals 1 or an individual owning a car given their income. Moreover, it is a linear function of the independent variables in the model.

Since this model predicts conditional probability and is linear, it has been named the Linear Probability Model.

Linear Probability Model: Problems

It seems like a good idea to estimate the above model with LPM, but this is not the case. The LPM or Linear Probability Model suffers from some serious problems:

Probability limits of 0 and 1

We know that the probability of any event lies between 0 and 1. Probability cannot exceed these limits of 0 and 1. A negative probability or a probability greater than 1 does not make sense. This brings us to the first problem of the LPM. When we apply OLS to a model with a binary dependent variable like the one specified earlier, the predictions do not necessarily adhere to the probability limits.

This means that the predicted probability from the Linear Probability Model can be negative or greater than 1. The dependent variable is a linear function of the independent variables and its predictions will not necessarily be bounded between the limits of 0 and 1.

Heteroscedasticity in Linear Probability Models

Homoscedasticity or constant residual variance is one of the most important assumptions of OLS. The tests of significance are not reliable when the residuals are not homoscedastic. On the other hand, heteroscedasticity is a situation of non-constant variance of residuals where the residuals are correlated with the independent variable. The OLS estimates are still unbiased but they are no longer efficient under heteroscedasticity.

The Linear Probability Model suffers from heteroscedasticity. The residuals from LPM do not have a constant variance. The variance of residuals in LPM is a function of the probability of success or Probability of X equals 1. In turn, the probability is a function of the dependent variables in the model. As a result, the variance of residuals is also a function of the independent variables in the LPM model. This further leads to a non-constant variance and heteroscedasticity.

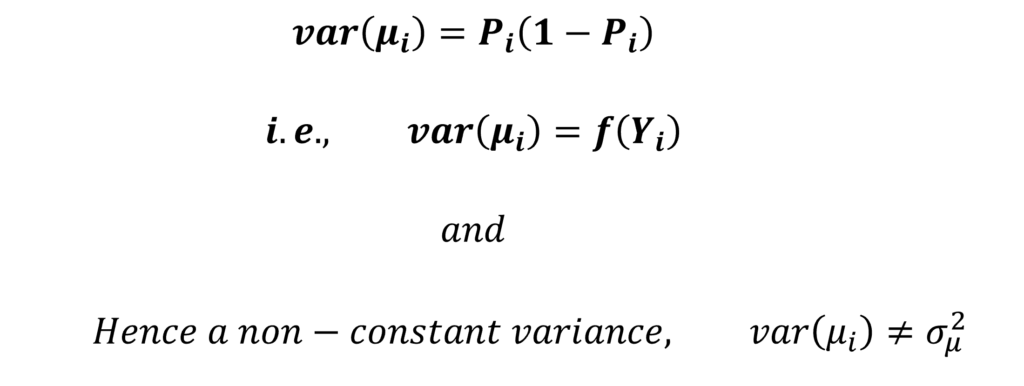
Assumption of Linearity

The linearity assumption is the biggest drawback of the Linear Probability Model. This means that LPM assumes a linear relationship between the dependent and the independent variables. In our example, the ownership of a car is a linear function of income.

Hence, this implies that an increase in income always leads to a constant increase in the probability of owning a car, irrespective of the income level. Therefore, it does not matter whether income increases from 10 to 11 or from 10000 to 10001, the probability will increase by the same constant amount with a 1 unit increase in income.

However, the effect income has on the ownership of a car will not be constant at different income levels. For instance, at a very low income level, the change in the probability of owning a new car should be low. This is because the individual may still not be able to afford a car, so the probability should not change much. However, after a certain income level, the change in the probability of owning a car will be higher with a 1 unit increase in income. Similarly, at very high incomes beyond a certain level, the effect of a 1 unit increase in income may be little on the probability of owning a car.

This gives us a non-linear type of relationship between income and car ownership. In response to the same 1 unit change in income, the probability will change slowly at low income levels, change faster as income level keeps increasing and finally change slowly again at very high income levels.

Therefore, the linearity assumption of LPM does not make much sense in the case of such models. Instead, we should model such relationships using non-linear type of functions.

Soliution to the problems of Linear Probability Model

As evident from the problems stated above, the LPM is not appropriate for models with binary dependent variables. We need a different structure to estimate such models. If we consider the problems carefully, we need 2 things to estimate such models:

• Probability must stay between 0 and 1
• A non-linear type of function, where the probability changes slowly as we approach extreme values of independent variables.

Both these conditions are met by the Sigmoid function and the Normal Cumulative Distribution Function (Normal CDF). The Sigmoid function is used to derive and estimate the Logit Model. Whereas, the Normal CDF is used in the Probit Model. Both these functions and models ensure that the probability does not exceed the limits of 0 and 1. Moreover, both the Sigmoid and Normal CDF are non-linear in nature. That is, the probability of the dependent variable will change slowly at extreme values of independent variables.

The Logit and Probit models use the Maximum Likelihood approach. To learn to derive the likelihood functions for Logit and Probit models, the goodness of fit, derive the marginal effects, estimate different types of marginal effects and the models in R and Stata, you can go to the links here: Logit and Probit Models and Goodness of fit for Logit and Probit Models.

---