Nelson’s low-level equilibrium trap model attempts to explain the reasons or factors that make it difficult for underdeveloped economies to raise their standard of living. It considers the role and linkages between population growth and per capita income. These linkages pull underdeveloped economies towards an equilibrium level characterised by low capital formation and per capita income. This develops into a situation of a trap where the economy is stable at a low level of per capita income. It becomes difficult to raise per capita income levels because the economy has a tendency to settle at that point.
The model by Nelson considers the role of savings for investment, population and income in his model. All of these variables are interlinked and their behaviour in response to per capita income can be demonstrated as follows:
Related Posts
- Vicious Circle of Poverty
- Kuznets’ Inverted-U Hypothesis
- Three Core Values of Development
- Lewis Model of Structural Change
- Fei and Ranis’ Model of Structural Change
Rate of savings, population and income growth
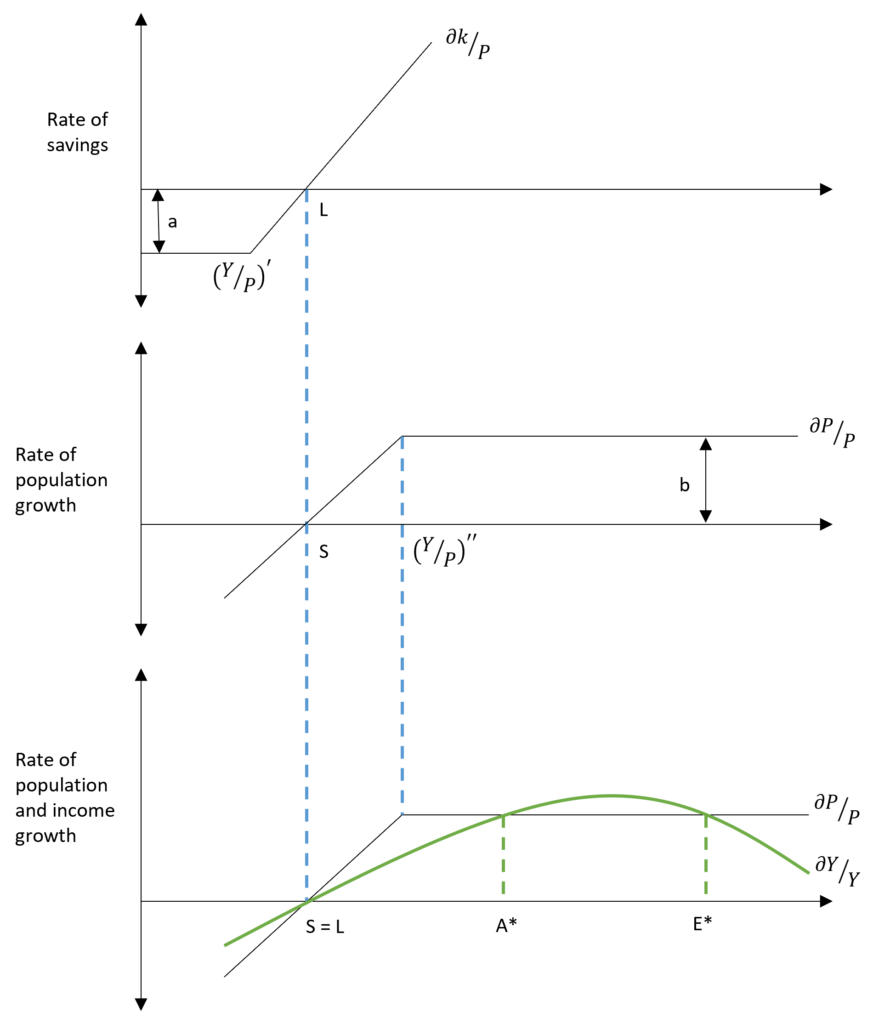
Rate of Savings Per Capita
Savings, here, refers to the amount of savings used for capital formation, i.e. savings for investment. The rate of savings per capita is related to income per capita in such a manner that at very low levels of per capita income (less than (Y/P)’ ), there is disinvestment in the economy. Therefore, the rate of savings per capita is negative and equal to ‘-a’. Beyond the (Y/P)’ level of per capita income, the rate of savings is a positive and linear function of per capita income. That is, the rate of savings per capita increases with an increase in per capita income. Point ‘L’ is the level of per capita income where the rate of savings per capita is zero.
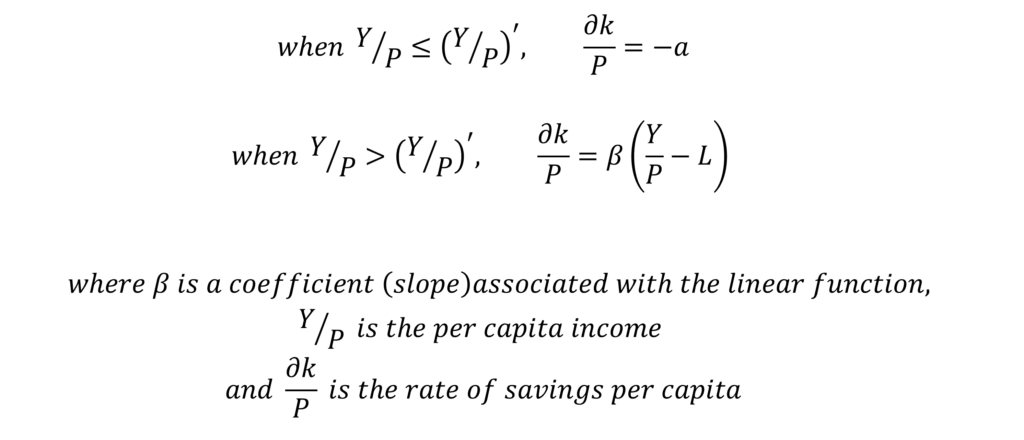
Rate of Population Growth
Initially, the rate of population growth rises with an increase in per capita income because of a falling death rate. With higher per capita income, people can afford better healthcare. Even the general standard of living improves leading to a decrease in the death rate. When the death rate falls to the minimum level, the rate of population growth becomes constant at that point.
As seen in the diagram, the population growth rate increases till per capita income rises to (Y/P)”. It becomes constant after reaching this level. Before point ‘S’, the population growth rate is negative as the death rate exceeds the birth date. However, the death rate falls with a rise in per capita income and the population growth rate is positive beyond point ‘S’.
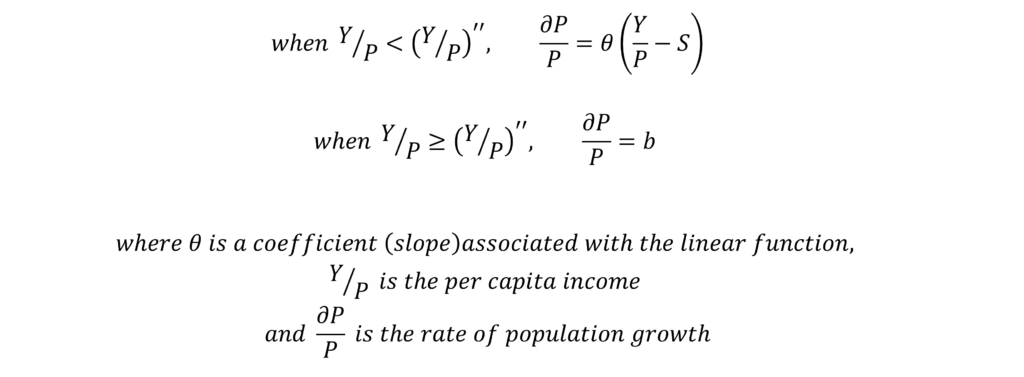
Total Income Growth
Total income or output is a function of labour and capital with technology assumed to be constant. The curve (dY/Y) represents the total income growth rate in the diagram. At point S=L, the population is stationary and the rate of savings for investment is zero. Therefore, the total income growth rate is zero at this point because both factors affecting total income (labour and capital) have zero growth rates.
Beyond this point, total income growth increases with a rise in per capita income because of the increasing population (and labour force) and positive savings rate growth. However, the population growth rate will reach its maximum point and the proportion of savings out of total income will become constant. Hence, total income growth will start to level after a certain point.
Eventually, the income growth rate will start falling. This happens because the marginal product will become negative due to the law of variable proportions as labour keeps increasing and technology remains constant.
The equilibrium trap
The point ‘S=L’ represents the low-level equilibrium trap. This is where the economy will tend to settle at a lower level of per capita income. If per capita income increases, growth in population rate is higher than the total income growth. This again drives the per capita income back to this point ‘S=L’. Any level of per capita income which is less than ‘A*’ will result in a fall of per capita income to the point of ‘S=L’. This happens because the growth rate of the population is greater than the income growth rate till point ‘A*’.
However, there is another point of stable equilibrium at ‘E*’. If per capita income increases beyond ‘A*’, then the economy will settle at point ‘E*’ where per capita income is high. Beyond point ‘A*’, per capita income will witness a steady rise because the growth rate of total income is greater than the population growth rate after point ‘A*’.
Escaping the Equilibrium Trap
There are 2 ways to escape the low-level equilibrium trap:
- Raise per capita income beyond A*: if the underdeveloped economies can somehow manage to increase the per capita income levels beyond this point, then the economy will automatically settle at a high per capita income level of E*. The “Big-Push” theories of development suggest this approach where a massive influx of investment can enable underdeveloped economies to go beyond this point A*. Thereby, bringing in a steady rise in per capita income after this point. However, this approach has a major drawback in that underdeveloped economies already lack investment and struggle from low-income levels. Therefore, it is nearly impossible to bring in such a huge investment.
- Shift total income growth curve upwards: by shifting the growth rate of total income (dY/Y) upwards and above the population growth rate (dP/P) curve, underdeveloped economies can bring a steady rise in per capita income. This happens because the income growth rate will be greater than the population growth rate. Hence, per capita income will keep rising. This can be achieved with improvement in technology or technological progress. Foreign direct investments can also help shift the income growth rate upwards.

criticism
- The theory assumes that an increase in per capita income leads to a fall in death rates and a rise in population growth rate. However, it ignores the measures that governments of underdeveloped economies take to control the birth rate and therefore, population growth. Increases in per capita income may not necessarily imply a rise in population growth rate. It completely ignores other factors that may influence population growth.
- The role of government policies is as important as per capita income in determining the level of investment within the economy. Additionally, foreign investment largely depends on the policies adopted by the state.
- It does not take time into consideration. Focus on time is absent even though population and income growth are generally seen as time series elements. There is no distinction made between short-run or long-run measures by underdeveloped economies in relation to these growth rates.
- It assumes technology to be constant. Not just per capita income, but technology and innovations play a massive role in determining the total income growth rate.

