To illustrate simultaneous equilibrium, we will consider a 2*2*2 model with two products (X and Y), two consumers (A and B) and two factors of production (L and K). The production possibility curve (PPC) will show the producer equilibrium. The PPC depicts efficient combinations of two goods (X and Y) that a firm can produce with given labour (L) and capital (K). The consumer equilibrium will be represented by indifference curves of both consumers A and B. Consumer equilibrium will be shown using an Edgeworth-Box diagram within the PPC.
Econometrics Tutorials with Certificates
conditions of consumer and producer equilibrium
In previous sections, we discussed consumer equilibrium and producer equilibrium conditions separately.
The conditions of consumer equilibrium can be expressed as:
MRS = PX / PY
In the Production Possibility Curve (PPC), the slope of the curve is given by:
MRT = MCX / MCY = PX / PY
The indifference curves show the trade-off (shown by MRS) between two goods. Each combination of goods on an indifference curve gives the same level of satisfaction to consumers. On the other hand, the PPC shows a trade-off (shown by MRT) between the production of those goods. Equilibrium cannot be achieved if these rates (MRT and MRS) are different because consumer satisfaction will not be maximized. When these rates are equal, the pattern of production will be the same as the consumer preferences.
simultaneous equilibrium
For simultaneous equilibrium to occur, the slope of indifference curves facing each consumer has to be the same as the slope of PPC. Therefore,
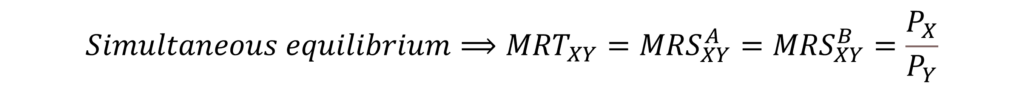
This equilibrium can be illustrated using PPC and Edgeworth-Box diagram as follows:
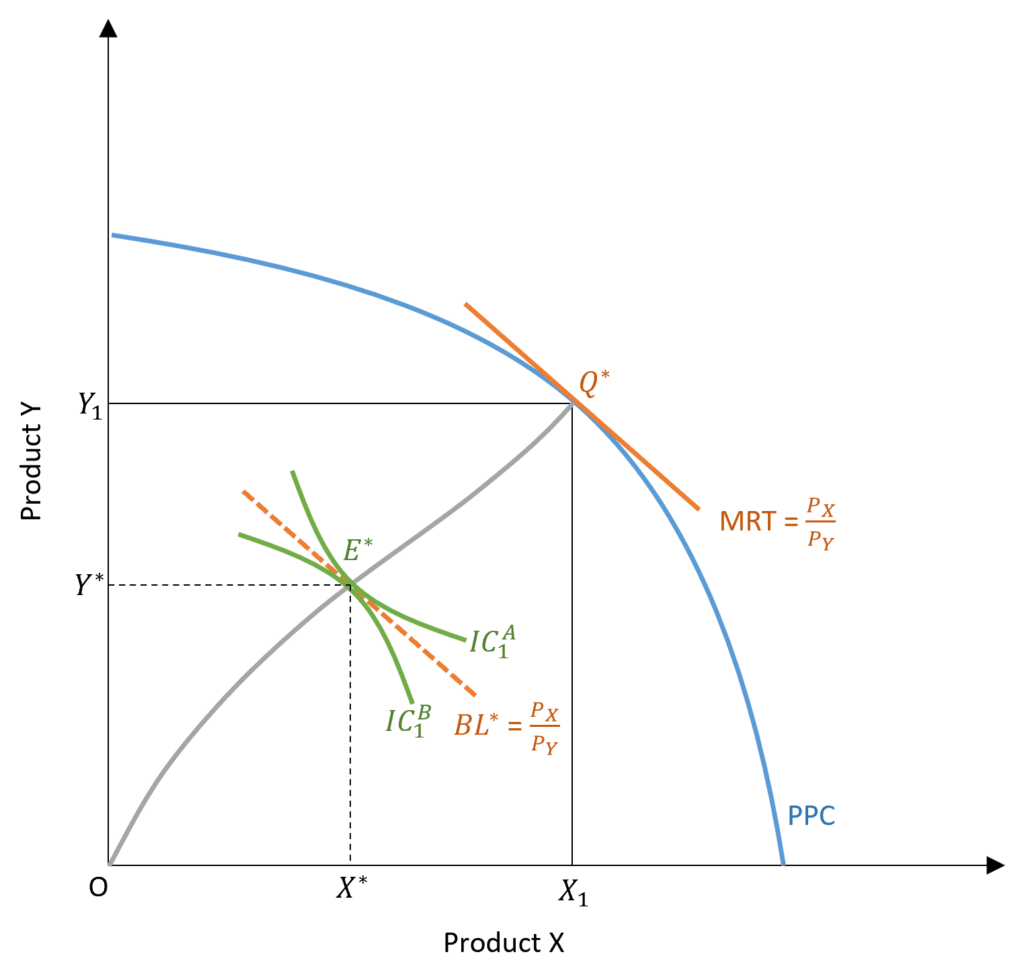
In the diagram, producer equilibrium is shown by point Q* on the PPC and consumer equilibrium occurs at E*. The slope of PPC (MRT) at point Q* is equal to the slope of indifference curves of consumers A and B (IC1A and IC1B) as well as the slope of budget line BL*.
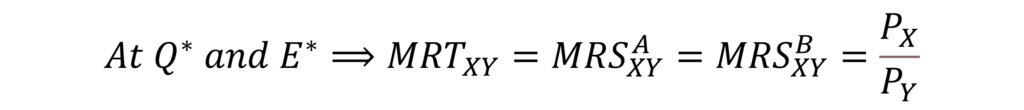
The producer equilibrium at Q* determines the total quantity produced of both goods X and Y, given the factors of production L and K. Total output of good X is given by OX1 and the total output of Y is equal to OY1.
Consumers A and B will be at equilibrium at E*. At this point, the indifference curves of both the consumers are tangent to each other and the budget line BL*. Out of the total output of both goods, consumer A will buy OX* and OY* quantity of goods X and Y respectively. The remaining output is purchased by consumers B, which is equal to X*X1 and Y*Y1 for goods X and Y respectively.
At this equilibrium, the slope of isoquants or MRTS of both goods will also be equal to the ratio of their prices:
MRTSLKX = MRTSLKY = PX / PY
Illustration: why equilibrium is at Q* and E*?
Suppose, the producer is operating at a different point on PPC. Then, the MRT and MRS of consumers will not be equal. As a result, the economy will be in disequilibrium as the equilibrium condition is not satisfied.
Case 1: MRT > MRS
Let us assume that MRT is 4 and MRS is 2. This means that the consumers are willing to purchase 2 units of Y by giving up 1 unit of X. Whereas, 4 extra units of Y can be produced by giving up 1 unit of X. A lot more units of Y can be produced by giving up a small amount of X. The consumers will increase their satisfaction by purchasing those extra units of Y because consumers will get 4 units of Y for every X foregone (i.e. more than 2 units of Y, which gave the same satisfaction as 1 unit of X consumed).
Therefore, it is beneficial to produce more of Y by giving up X. A greater quantity of good X is being produced than is required. And, satisfaction can be increased by producing more of Y and foregoing some of good X.
The producers will go on producing more of Y by giving up X till the MRT and MRS become equal. Hence, by giving up an extra unit of X, consumers will purchase the extra quantity of Y. At equilibrium, this will be the same as the extra quantity of Y produced by giving up the production of a unit of X.
Case 2: MRT < MRS
Conversely, if MRT < MRS, it implies that the output of Y is greater than what is desired by consumers. In this case, firms will forego the production of Y to produce more of X. This process will go on till the MRT of producers is equal to the MRS of consumers. At this stage, maximum satisfaction will be attained.
This equilibrium can also be termed the equilibrium of production and exchange. It leads to an efficient allocation of resources because available labour and capital are allocated efficiently by the PPC, and the output of both products is maximized. Further, in the case of consumers, the exchange of products is such that the utility or satisfaction of both consumers is maximized.
Econometrics Tutorials with Certificates
This website contains affiliate links. When you make a purchase through these links, we may earn a commission at no additional cost to you.


