The Indirect Least Squares (ILS) is a method used to estimate simultaneous equation models that are exactly identified. Moreover, it is a single equation method because it is applied to each equation of the system one by one. That is, all the equations are not estimated simultaneously. However, this method does not apply to overidentified models as it will not give unique estimates of the structural coefficients of the model. Hence, the Two-stage least squares (2SLS) method is used to estimate overidentified models.
Econometrics Tutorials with Certificates
reduced form method for indirect least squares
ILS involves the use of the Reduced-Form Method in which the endogenous variables are expressed in terms of all the exogenous variables. This implies that we manipulate the equations of the simultaneous equation model in such a way that we only have all the endogenous variables as dependent variables and all the exogenous variables as independent variables. As a result, it helps eliminate the two-way causation that we observe in simultaneous equation models.
Each Reduced-Form equation that we generate can be estimated using OLS. Therefore, OLS is applied to every equation separately or one by one to obtain the Reduced-Form coefficients. Moreover, these Reduced-Form coefficients are a combination of the coefficients of structural parameters. The structural parameters are the coefficients of the original simultaneous equation model. Hence, the structural coefficients can be derived from the Reduced-Form coefficients. Let us illustrate the estimation of structural and reduced form coefficients using ILS with an example.
ILS: Estimating Structural and reduced form coefficients
Step 1: Identification using Rank and Order Conditions
Let us consider the following hypothetical model:
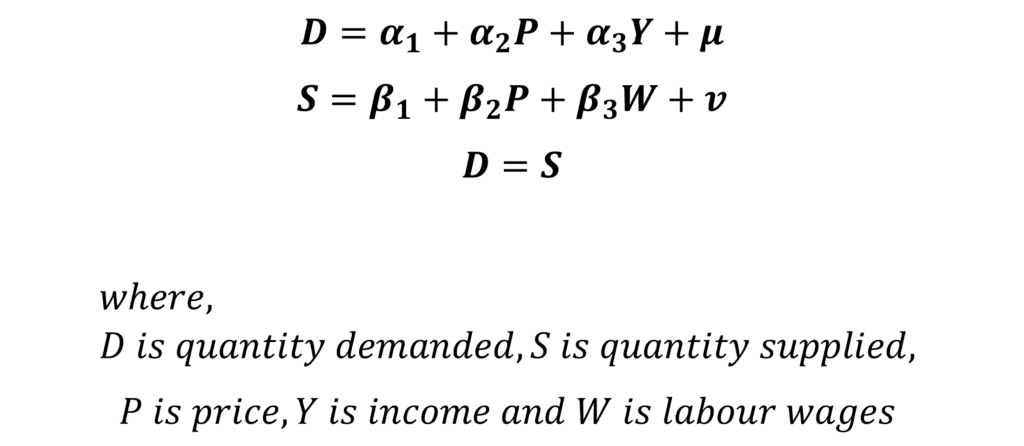
This model is complete because we have 3 endogenous variables and 3 equations. Furthermore, Y and W are exogenous variables. These equations are the Structural equations and their coefficients are referred to as the Structural parameters or coefficients.
Note: this is a hypothetical model. In practice, we must make sure that the structural equations of the simultaneous equation model make economic sense. Hence, the overall model and its relationships should include variables based on economic theory or background.
Demand Function: we can easily determine that the demand equation is exactly identified with the help of Rank and Order Conditions of Identification.
Supply Function: similarly, the supply equation is also exactly identified.
Exactly identified models have to be estimated using the Indirect Least Squares. You can learn about the application of Rank and Order Conditions from the post on Identification: Rank and Order Conditions.
Step 2: Obtain Reduced Form Equations and coefficients
We have observed that the demand and supply functions are exactly identified. Hence, we can estimate the structural coefficients using Indirect Least Squares (ILS). We need to construct the Reduced-Form equations which express the endogenous variables in terms of all the exogenous variables. That is, we need to have endogenous variables on the left side and exogenous variables on the right side of the equations. This can be accomplished with the manipulation of the equations of our model.

We have expressed the endogenous variable Pt as the dependent variable and exogenous variables of our structural model Yt and Wt as independent variables.
Further, we can substitute this equation into the Demand function and simplify it to get:
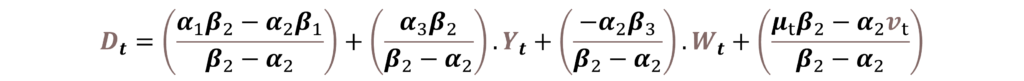
These reduced-form equations can also be expressed as:
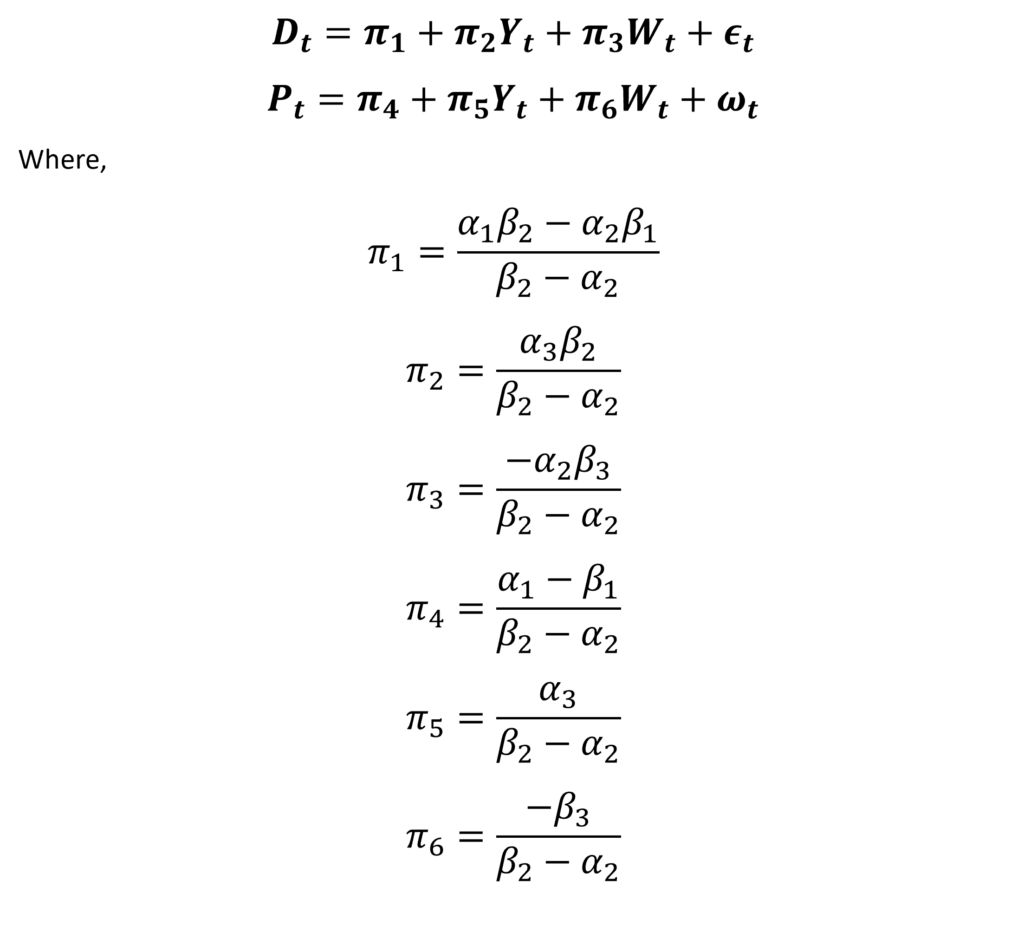
Hence, the Reduced-Form coefficients are a non-linear combination of structural parameters. Therefore, we can obtain the estimates of these Reduced-Form coefficients using OLS. This is because we have eliminated the two-way causation by expressing endogenous variables in terms of exogenous variables. We can apply OLS to the above equations separately to get the values of the reduced-form coefficients.
Step 3: Obtain the values of Structural Parameters
From the estimates of these Reduced-Form coefficients, we can also obtain the estimates of structural parameters. We have 6 structural parameters and 6 Reduced-Form coefficients expressed in terms of structural parameters. Therefore, we can solve the system of equations defining Reduced-Form coefficients. It is possible to get the estimates of structural parameters by manipulating the equations as:

Here, we have the structural parameters further expressed in terms of Reduced-Form coefficients. Therefore, we can obtain the estimates of structural parameters of our simultaneous equation model using Indirect Least Squares or ILS.
Implementing Indirect Least Squares
In the previous steps, we derived the Reduced-Form equations and Reduced-Form coefficients. Now, we apply OLS to both our Reduced-Form equations separately and obtain the estimates of Reduced-Form coefficients.
| Dependent variable = Dt | ||
| Independent variables | Coefficients | |
| Yt | 0.57 | |
| Wt | 0.95 | |
| Constant | 0.82 | |
| Dependent variable = Pt | ||
| Yt | 0.98 | |
| Wt | 0.48 | |
| Constant | 1.06 |
Since we have the values of all Reduced-Form coefficients from OLS, we can use these to obtain the structural parameters. Therefore, we can simply plug in the values of Reduced-Form coefficients into the equations we derived earlier to obtain the structural parameters:
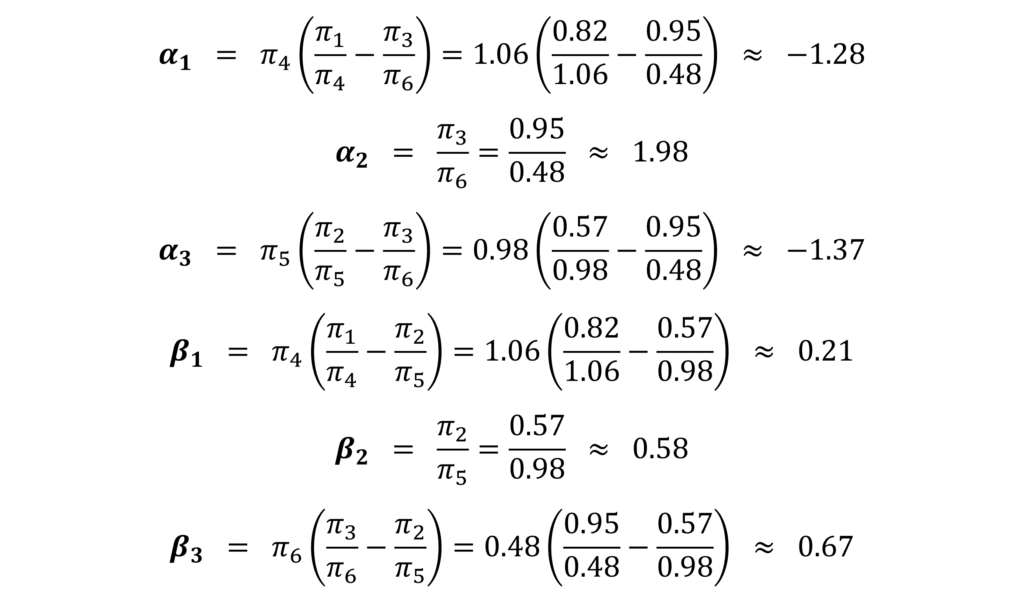
Indirect Least Squares: Interpretation
Total Effects
We have estimated Reduced-Form coefficients as well as the structural parameters of our simultaneous equation model using Indirect Least Squares (ILS).
The Reduced-Form coefficients represent the “Total Effect” of exogenous variables on the endogenous variable of the Reduced-Form equation. Consider the first Reduced-Form equation of demand:
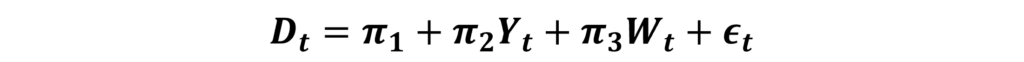
We know that π3=0.95, which shows the “Total Effect” of labour wages on demand. Similarly, π2 (0.57) shows the “Total Effect” of income (Yt)on demand.
Similarly, Reduced-Form coefficients π5 (0.98) and π6 (0.48) represent the “Total Effect” of income (Yt) and labour wages (Wt) respectively on the endogenous variable of Price (Pt).
Direct Effects
Total Effect = Direct Effect + Indirect Effect
We observed that the “Total Effects” are shown by Reduced-Form coefficients. The “Direct Effects”, on the other hand, are shown by the structural parameters.
We also derived the structural parameters using the Reduced-Form coefficients. We know that α2=1.98, which shows the “Direct Effect” of variable Pt (price) on demand. Similarly, α3 (-1.37) shows the “Direct Effect” of income (Yt) on demand.
Therefore, structural parameters show “Direct Effects”, whereas, Reduced-Form coefficients show “Total Effects”.
Indirect Effects
Furthermore, we can also analyze the “Direct” and “Indirect” effects within the “Total Effects”. Suppose, we want to analyse the “Total Effect” of π2, which shows the “Total Effect” of Yt (Income) on Demand.

In addition to the “Direct Effect” (shown by α3), demand is also affected indirectly through price. This indirect effect takes place in a manner that Yt (income) also influences Pt (price), which in turn also affects demand (D). We can further observe this with the presence of structural parameters of β2 and α2 within the “Total Effect”. Hence, the indirect effect shows how Yt influences demand (D) through Pt.
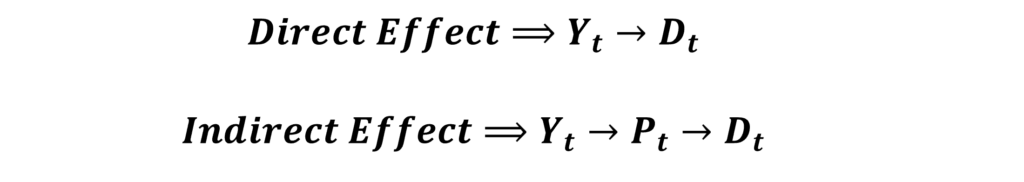
For the purpose of forecasting, we can simply use the Reduced-Form coefficients because we are only concerned about the overall or “total” effect.
drawback of indirect least squares
If the number of equations and parameters in the model is large, it can be further difficult to derive Reduced-Form coefficients. That is, the process will become too complex and cumbersome. Moreover, most of the simultaneous equation models are overidentified and we rarely encounter exactly identified models. Since Indirect Least Squares cannot be applied to overidentified models, their use is limited in practice.
Econometrics Tutorials with Certificates
This website contains affiliate links. When you make a purchase through these links, we may earn a commission at no additional cost to you.




