Ramsey’s Regression Specification Error Test, or Ramsey’s RESET Test, is often used to test for functional form misspecification in regression models. A model suffers from functional form misspecification when we do not completely account for the relationship between the independent and dependent variables. Suppose the true relationship between variables is quadratic in nature, but we only include a linear relationship in the model; then the regression will suffer from functional form misspecification.
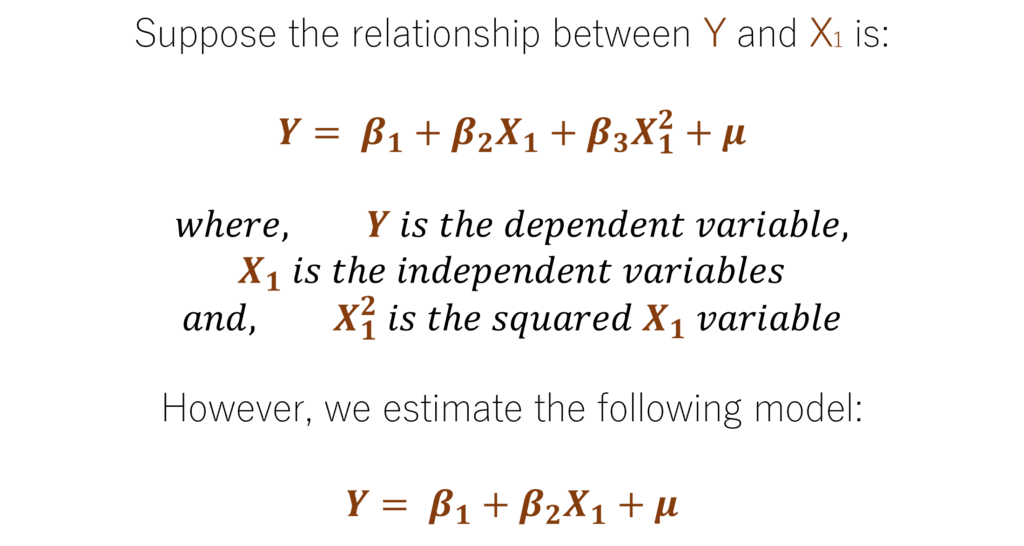
We are committing a functional form misspecification by estimating the second equation instead of the first. Moreover, the estimates from the 2nd equation will generally be biased. This is because we have excluded X12 and β3 from the model.
Econometrics Tutorials with Certificates
The logic behind Ramsey’s RESET Test
In general, we can use the F test to compare 2 models by testing for joint exclusion restrictions. Hence, the unrestricted model would include all the independent variables and the quadratic or non-linear terms associated with those independent variables. The restricted model would include only the independent variables and exclude all the quadratic and non-linear terms. Then, we can compare the restricted and unrestricted models to test the joint significance of all the quadratic and non-linear terms.
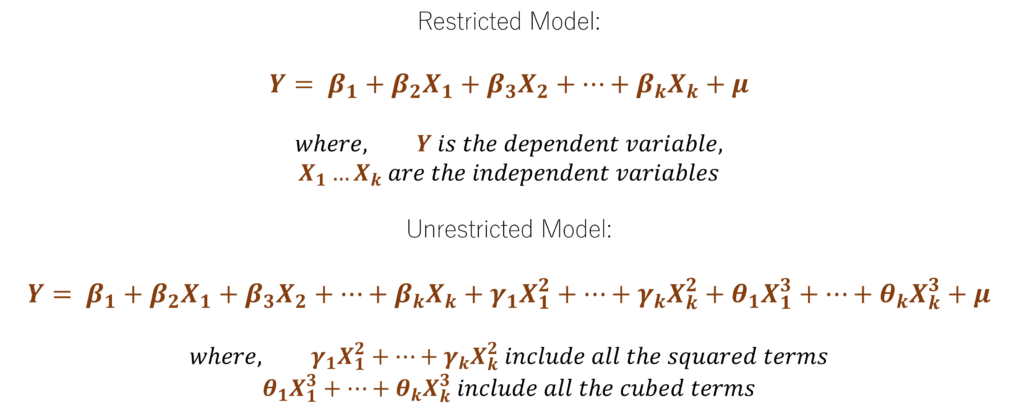
Using the above Restricted and Unrestricted models, we can apply the F-test to check the joint significance of the squared and cubed terms and their coefficients γ1,…, γk, θ1,…, θk.
However, there are some clear disadvantages to this approach:
- We have only included the squared and cubed terms in the Unrestricted Model. These are not the only non-linear terms or functional forms that might cause misspecification. We cannot include all the different forms of independent variables without consuming too many degrees of freedom.
- Even with only the squared and cubed terms, this method will consume a lot of degrees of freedom if we have many independent variables. Suppose we have 10 independent variables, then we will have to include an additional 10 squared terms and 10 cubed terms in the Unrestricted Model. This also implies that we have to estimate as many coefficients, thus consuming massive degrees of freedom.
To solve these problems, Ramsey developed the RESET Test, which tries to overcome these problems and still provide us with a meaningful test for functional form misspecification.
Application of Ramsey’s RESET Test
Step 1: Estimate the Original Restricted Model
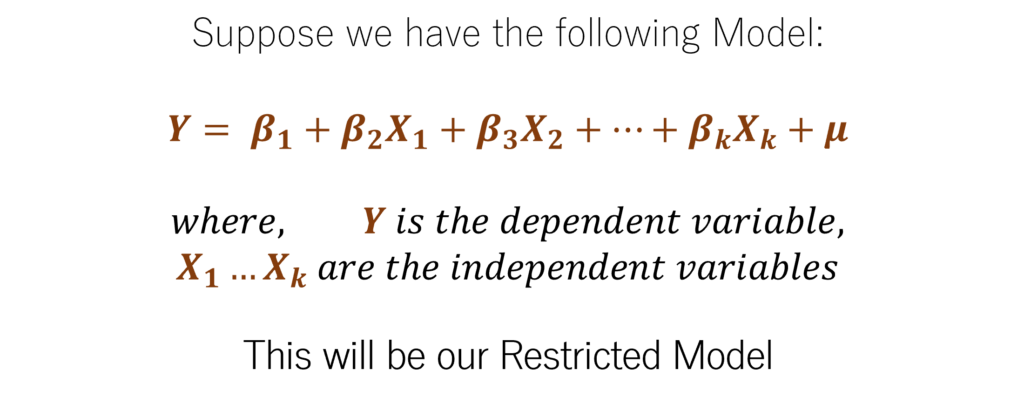
The model can have any number of independent variables, however, this restricted model will not have any quadratic or non-linear forms of the independent variables.
Step 2: Estimate the Predicted values of the dependent variable
Using the results of the Original Restricted Model in Step 1, we can estimate the predicted values of the dependent variables.

From the predicted values, we can also create 2 additional variables: the square and cube of the predicted values.
Step 3: Estimate the Unrestricted Model
In the Ramsey’s RESET Test, we use the squares and cubes of the fitted or predicted values in the Unrestricted Model. That is, instead of including the squares, cubes and other non-linear forms of independent variables, we use the squares and cubes of predicted values. Since these predicted values are obtained from the Original Restricted Model, we know that they are a function of the independent variables X1, X2,…, Xk.
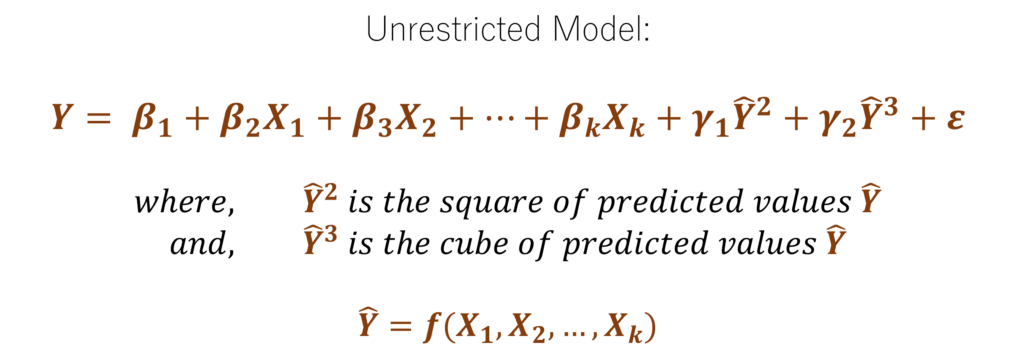
Moreover, we can include other forms of the fitted or predicted values in the Unrestricted Model. We have only included the squared and cubed fitted values because they have been observed to be useful in most applications. In this model, we are also not interested in the coefficient estimates. We only want to test whether the original model may have missed important non-linear relationships. The squared and cubed fitted or predicted values are simply the nonlinear functions of the independent variables.
Step 4: Apply the F-test
Finally, we can apply the F-test using the Residual Sum of Squares (RSS) from the Restricted and Unrestricted Models.

The F-statistic follows the F distribution with df1 = 2 and df2 = n – k – 3 in large samples. It is important to note here that you will have to adjust these degrees of freedom if you wish to include more nonlinear forms of the fitted or predicted values.
If the F-statistic is greater than the critical values, we can reject the null hypothesis and conclude that there is some form of functional form misspecification in the original model. Hence, we must include some nonlinear forms of the independent variables in the model.
Drawbacks of Ramsey’s RESET Test
- If the null hypothesis is rejected and there is functional form misspecification, the test does not give us any information about how to proceed or tell us what kind of non-linearity is causing the problem. That is, it does not tell us what type of non-linearities we need to account for in the model.
- Some argue that the RESET test can also be a test for omitted variables. However, the test generally has no power in detecting omitted variables and should not be used for this purpose.
- The RESET test also has no power to detect heteroscedasticity and should not be used for such a purpose. It is a test for functional form misspecification only.
Although the test has drawbacks, it provides us with a method to check for functional form misspecification in the model. Hence, it is a valuable tool if we suspect nonlinear relationships among the variables.
Econometrics Tutorials with Certificates
This website contains affiliate links. When you make a purchase through these links, we may earn a commission at no additional cost to you.


